java tutorial - Merge sort algorithm in Java - java programming - learn java - java basics - java for beginners
Learn java - java tutorial - Merge sort algorithm in Java - java examples - java programs
Merge sort algorithm:
- Merge Sort is a Divide and Conquer algorithm. It separate input array in two parts, and then merge two sorted parts.
- The merge() function is used for merging two parts.
- It is a kind of Divide and Conquer algorithm in computer programming.
- It is one of the best popular sorting algorithms and a great method to develop confidence in creating recursive algorithms.
Applications of Merge Sort :
- Merge Sort is used for sorting linked lists in O(nLogn)time.
- The case of linked list is different mainly due to variance in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes not nearby in memory. In linked list, we can insert items in the mid in O(1) additional space and O(1) time. The merge operation of merge sort can be executed without further space for linked lists.
- Merge sort access data in order and the need of random access is low.
- Inversion Count Problem
- It is used in External Sorting.
Divide and Conquer Strategy :
- • We divide a problem into subproblems. When the solution to for each subproblem is prepared, we 'combine' the results from the subproblems to solve the main problem.
- • Suppose we had to sort an array A. A subproblem would be to sort a sub-section of this array initial at index p and ending at index r, denoted as A[p..r].
Divide :
- • If q is the half-way point among p and r, then we can separate the subarray A[p..r] into two arrays A[p..q] and A[q+1, r].
Conquer :
- • In the conquer step, we try to sort both the subarrays A[p..q] and A[q+1, r]. If we haven't yet reached the base case, we again divide both these subarrays and try to sort them.
Combine :
- • When the conquer step reaches the base step and we get two sorted subarrays A[p..q] and A[q+1, r] for array A[p..r], we combine the results by creating a sorted array A[p..r] from two sorted subarrays A[p..q] and A[q+1, r].
Sample Code:
public class kaashiv_infotech
{
private static void merge(int[] numbers, int first, int n1, int n2)
{
int[] temp = new int[n1+n2];
int copied = 0, copied1 = 0, copied2 = 0;
while((copied1 < n1) && (copied2 < n2))
{
if (numbers[first + copied1] < numbers[first + n1 + copied2])
temp[copied++] = numbers[first + copied1++];
else
temp[copied++] = numbers[first + n1 + copied2++];
}
while(copied1 < n1)
temp[copied++] = numbers[first + copied1++];
while(copied2 < n2)
temp[copied++] = numbers[first + n1 +copied2++];
for(int i = 0; i < n1+n2; i++)
numbers[first + i] = temp[i];
}
public static void mergeSort(int[] numbers, int first, int last)
{
int n1, n2;
if (last > 1){
n1 = last/2;
n2 = last - n1;
mergeSort(numbers, first, n1);
mergeSort(numbers, first + n1, n2);
merge(numbers, first, n1, n2);
}
}
public static void printArray(int[] numbers)
{
for(int i = 0 ; i < numbers.length; i++)
{
System.out.print(numbers[i] + " ");
}
System.out.println("");
}
public static void main(String[] args)
{
int[] list = {14,23,11,56,67,34,12,7,12,8,9,23};
System.out.println("Before Merge sort");
printArray(list);
System.out.println("\nAfter Merge sort");
mergeSort(list, 0, list.length);
printArray(list);
}
}
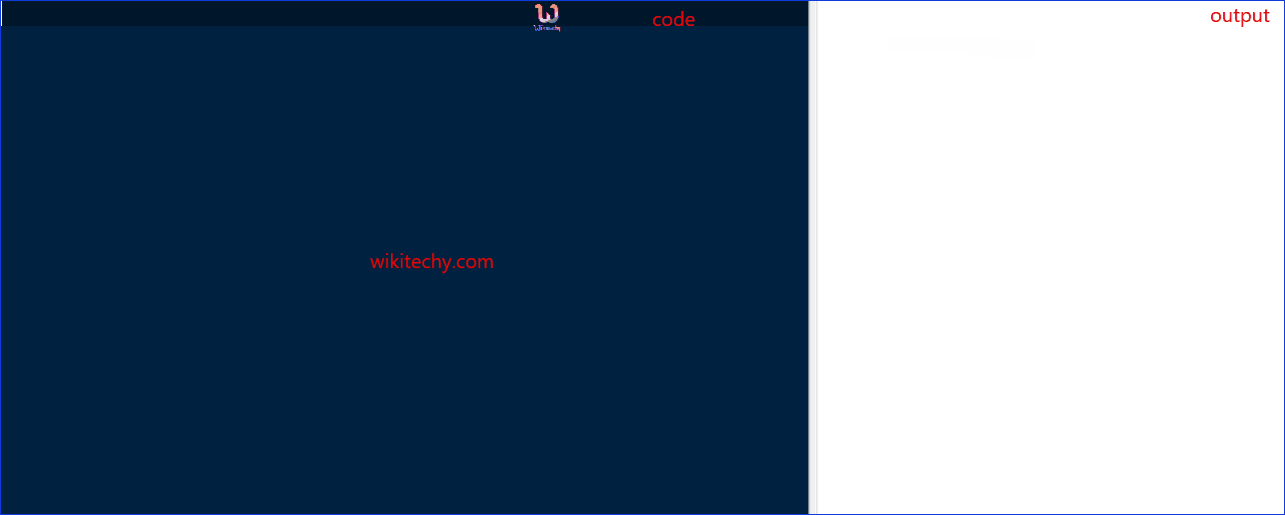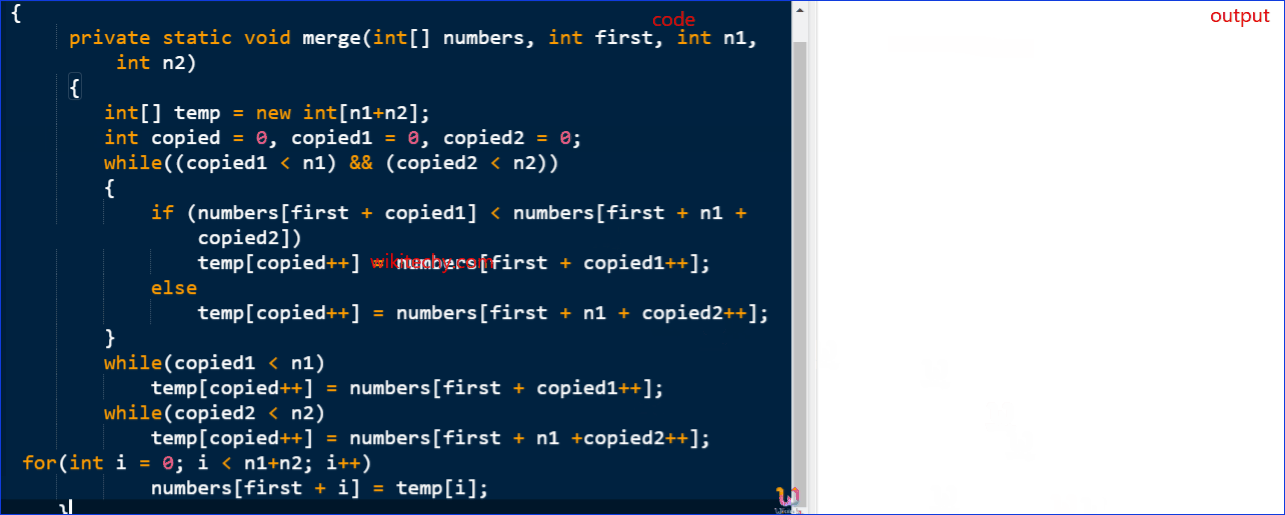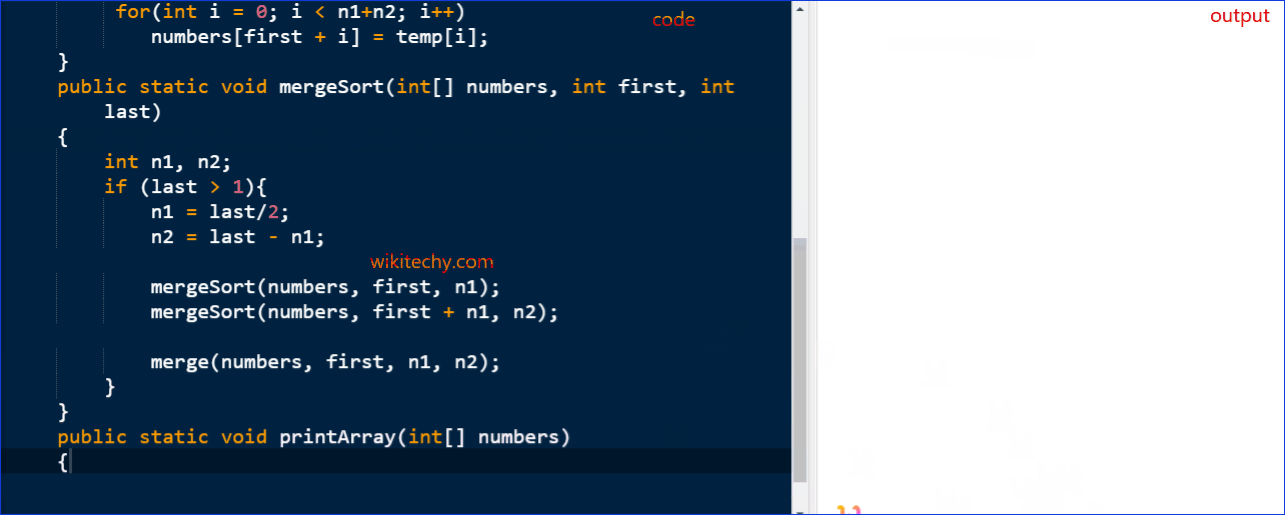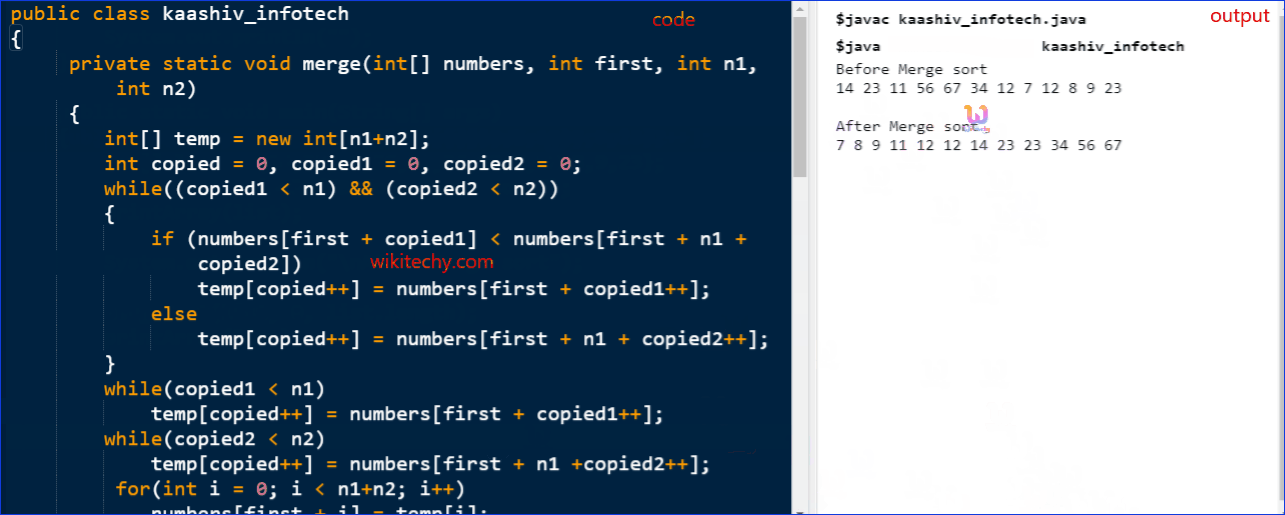
Output:
Before Merge sort
14 23 11 56 67 34 12 7 12 8 9 23
After Merge sort
7 8 9 11 12 12 14 23 23 34 56 67 