Given a directed and two vertices ‘u’ and ‘v’ in it, find shortest path from ‘u’ to ‘v’ with exactly k edges on the path.
The graph is given as adjacency matrix representation where value of graph[i][j] indicates the weight of an edge from vertex i to vertex j and a value INF(infinite) indicates no edge from i to j.
For example consider the following graph. Let source ‘u’ be vertex 0, destination ‘v’ be 3 and k be 2. There are two walks of length 2, the walks are {0, 2, 3} and {0, 1, 3}. The shortest among the two is {0, 2, 3} and weight of path is 3+6 = 9.
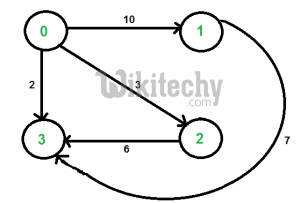
The idea is to browse through all paths of length k from u to v using the approach discussed in the previous post and return weight of the shortest path. A simple solution is to start from u, go to all adjacent vertices and recur for adjacent vertices with k as k-1, source as adjacent vertex and destination as v. Following are C++ and Java implementations of this simple solution.
[ad type=”banner”]
Java Programming
// Dynamic Programming based Java program to find shortest path
// with exactly k edges
import java.util.*;
import java.lang.*;
import java.io.*;
class ShortestPath
{
// Define number of vertices in the graph and inifinite value
static final int V = 4;
static final int INF = Integer.MAX_VALUE;
// A naive recursive function to count walks from u to v
// with k edges
int shortestPath(int graph[][], int u, int v, int k)
{
// Base cases
if (k == 0 && u == v) return 0;
if (k == 1 && graph[u][v] != INF) return graph[u][v];
if (k <= 0) return INF;
// Initialize result
int res = INF;
// Go to all adjacents of u and recur
for (int i = 0; i < V; i++)
{
if (graph[u][i] != INF && u != i && v != i)
{
int rec_res = shortestPath(graph, i, v, k-1);
if (rec_res != INF)
res = Math.min(res, graph[u][i] + rec_res);
}
}
return res;
}
public static void main (String[] args)
{
/* Let us create the graph shown in above diagram*/
int graph[][] = new int[][]{ {0, 10, 3, 2},
{INF, 0, INF, 7},
{INF, INF, 0, 6},
{INF, INF, INF, 0}
};
ShortestPath t = new ShortestPath();
int u = 0, v = 3, k = 2;
System.out.println("Weight of the shortest path is "+
t.shortestPath(graph, u, v, k));
}
}
Output:
Weight of the shortest path is 9
The worst case time complexity of the above function is O(Vk) where V is the number of vertices in the given graph. We can simply analyze the time complexity by drawing recursion tree. The worst occurs for a complete graph. In worst case, every internal node of recursion tree would have exactly V children.
We can optimize the above solution using Dynamic Programming. The idea is to build a 3D table where first dimension is source, second dimension is destination, third dimension is number of edges from source to destination, and the value is count of walks. Like other Dynamic Programming problems, we fill the 3D table in bottom up manner.
[ad type=”banner”]
Java programming
// Dynamic Programming based Java program to find shortest path with
// exactly k edges
import java.util.*;
import java.lang.*;
import java.io.*;
class ShortestPath
{
// Define number of vertices in the graph and inifinite value
static final int V = 4;
static final int INF = Integer.MAX_VALUE;
// A Dynamic programming based function to find the shortest path
// from u to v with exactly k edges.
int shortestPath(int graph[][], int u, int v, int k)
{
// Table to be filled up using DP. The value sp[i][j][e] will
// store weight of the shortest path from i to j with exactly
// k edges
int sp[][][] = new int[V][V][k+1];
// Loop for number of edges from 0 to k
for (int e = 0; e <= k; e++)
{
for (int i = 0; i < V; i++) // for source
{
for (int j = 0; j < V; j++) // for destination
{
// initialize value
sp[i][j][e] = INF;
// from base cases
if (e == 0 && i == j)
sp[i][j][e] = 0;
if (e == 1 && graph[i][j] != INF)
sp[i][j][e] = graph[i][j];
// go to adjacent only when number of edges is
// more than 1
if (e > 1)
{
for (int a = 0; a < V; a++)
{
// There should be an edge from i to a and
// a should not be same as either i or j
if (graph[i][a] != INF && i != a &&
j!= a && sp[a][j][e-1] != INF)
sp[i][j][e] = Math.min(sp[i][j][e],
graph[i][a] + sp[a][j][e-1]);
}
}
}
}
}
return sp[u][v][k];
}
public static void main (String[] args)
{
/* Let us create the graph shown in above diagram*/
int graph[][] = new int[][]{ {0, 10, 3, 2},
{INF, 0, INF, 7},
{INF, INF, 0, 6},
{INF, INF, INF, 0}
};
ShortestPath t = new ShortestPath();
int u = 0, v = 3, k = 2;
System.out.println("Weight of the shortest path is "+
t.shortestPath(graph, u, v, k));
}
}
Output:
Weight of the shortest path is 9
[ad type=”banner”]