Given a Weighted Directed Acyclic Graph and a source vertex in the graph, find the shortest paths from given source to all other vertices.
For a general weighted graph, we can calculate single source shortest distances in O(VE) time using Bellman–Ford Algorithm. For a graph with no negative weights, we can do better and calculate single source shortest distances in O(E + VLogV) time using Dijkstra’s algorithm. Can we do even better for Directed Acyclic Graph (DAG)? We can calculate single source shortest distances in O(V+E) time for DAGs. The idea is to use Topological Sorting.

We initialize distances to all vertices as infinite and distance to source as 0, then we find a topological sorting of the graph. Topological Sorting of a graph represents a linear ordering of the graph (See below, figure (b) is a linear representation of figure (a) ). Once we have topological order (or linear representation), we one by one process all vertices in topological order. For every vertex being processed, we update distances of its adjacent using distance of current vertex.

[ad type=”banner”]

Following figure is taken from this source. It shows step by step process of finding shortest paths.

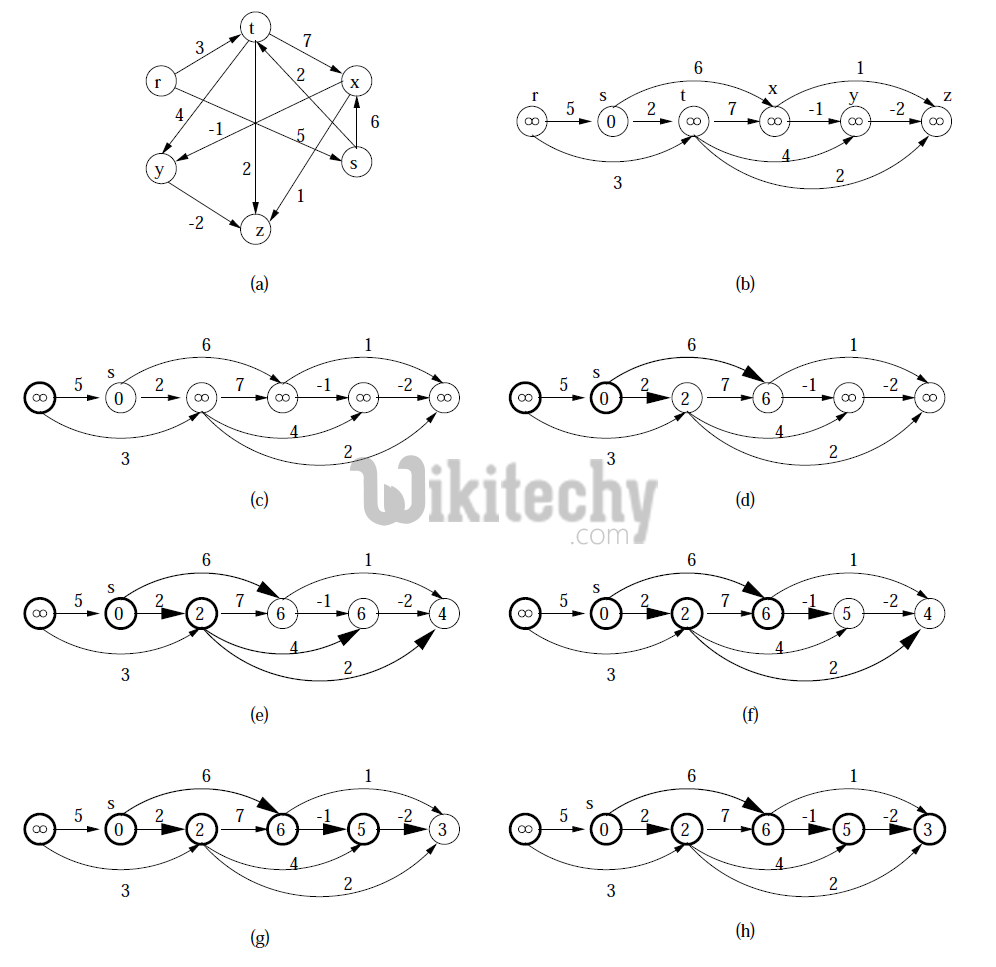Shortest Path-Shortest Path in Directed Acyclic GraphFollowing is complete algorithm for finding shortest distances.
1) Initialize dist[] = {INF, INF, ….} and dist[s] = 0 where s is the source vertex.
2) Create a toplogical order of all vertices.
3) Do following for every vertex u in topological order.
Do following for every adjacent vertex v of u
if (dist[v] > dist[u] + weight(u, v))
dist[v] = dist[u] + weight(u, v)

[ad type=”banner”]

Python Programming

# Python program to find single source shortest paths
# for Directed Acyclic Graphs Complexity :OV(V+E)
from collections import defaultdict
 
# Graph is represented using adjacency list. Every
# node of adjacency list contains vertex number of
# the vertex to which edge connects. It also contains
# weight of the edge
class Graph:
    def __init__(self,vertices):
 
        self.V = vertices # No. of vertices
 
        # dictionary containing adjacency List
        self.graph = defaultdict(list)
 
    # function to add an edge to graph
    def addEdge(self,u,v,w):
        self.graph[u].append((v,w))
 
 
    # A recursive function used by shortestPath
    def topologicalSortUtil(self,v,visited,stack):
 
        # Mark the current node as visited.
        visited[v] = True
 
        # Recur for all the vertices adjacent to this vertex
        if v in self.graph.keys():
            for node,weight in self.graph[v]:
                if visited[node] == False:
                    self.topologicalSortUtil(node,visited,stack)
 
        # Push current vertex to stack which stores topological sort
        stack.append(v)
 
 
    ''' The function to find shortest paths from given vertex.
        It uses recursive topologicalSortUtil() to get topological
        sorting of given graph.'''
    def shortestPath(self, s):
 
        # Mark all the vertices as not visited
        visited = [False]*self.V
        stack =[]
 
        # Call the recursive helper function to store Topological
        # Sort starting from source vertice
        for i in range(self.V):
            if visited[i] == False:
                self.topologicalSortUtil(s,visited,stack)
 
        # Initialize distances to all vertices as infinite and
        # distance to source as 0
        dist = [float("Inf")] * (self.V)
        dist[s] = 0
 
        # Process vertices in topological order
        while stack:
 
            # Get the next vertex from topological order
            i = stack.pop()
 
            # Update distances of all adjacent vertices
            for node,weight in self.graph[i]:
                if dist[node] > dist[i] + weight:
                    dist[node] = dist[i] + weight
 
        # Print the calculated shortest distances
        for i in range(self.V):
            print ("%d" %dist[i]) if dist[i] != float("Inf") else  "Inf" ,
 
 
g = Graph(6)
g.addEdge(0, 1, 5)
g.addEdge(0, 2, 3)
g.addEdge(1, 3, 6)
g.addEdge(1, 2, 2)
g.addEdge(2, 4, 4)
g.addEdge(2, 5, 2)
g.addEdge(2, 3, 7)
g.addEdge(3, 4, -1)
g.addEdge(4, 5, -2)
 
# source = 1
s = 1
 
print ("Following are shortest distances from source %d " % s)
g.shortestPath(s)

 

Output:

Following are shortest distances from source 1
INF 0 2 6 5 3

Time Complexity: Time complexity of topological sorting is O(V+E). After finding topological order, the algorithm process all vertices and for every vertex, it runs a loop for all adjacent vertices. Total adjacent vertices in a graph is O(E). So the inner loop runs O(V+E) times. Therefore, overall time complexity of this algorithm is O(V+E).

[ad type=”banner”]

Categorized in:

AlgorithmPYTHON

Tagged in:

, , , , , , , , , , , ,