Implementation Dequeue Using Circular Array:

Dequeue or Double Ended Queue is a generalized version of Queue data structure that allows insert and delete at both ends.In previous post we had discussed introduction of dequeue. Now in this post we see how we implement dequeue Using circular array.

Operations on Dequeue:

Mainly the following four basic operations are performed on queue:
insertFront(): Adds an item at the front of Dequeue.
insertRear(): Adds an item at the rear of Dequeue.
deleteFront(): Deletes an item from front of Dequeue.
deleteRear(): Deletes an item from rear of Dequeue.

In addition to above operations, following operations are also supported
getFront(): Gets the front item from queue.
getRear(): Gets the last item from queue.
isEmpty(): Checks whether Dequeue is empty or not.
isFull(): Checks whether Dequeue is full or not.

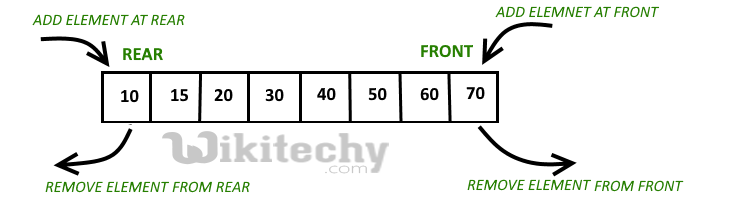
Queue-Data Structure-Implementation of Deque using circular array

[ad type=”banner”]

Circular array implementation dequeue 

For implementing dequeue, we need to keep track of two indices, front and rear. We enqueue(push) an item at the rear or the front end of queue and dequeue(pop) an item from both rear and front end.

Working

1. Create an empty array ‘arr’ of size ‘n’
initialize front = -1 , rear = 0
Inserting First element in dequeue either front end or read end they both lead to the same result.

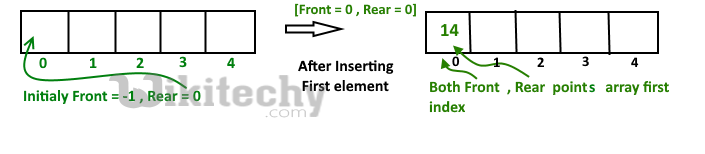
Queue-Data Structure Implementation of Deque using circular array

after insert Front Points = 0 and Rear points = 0

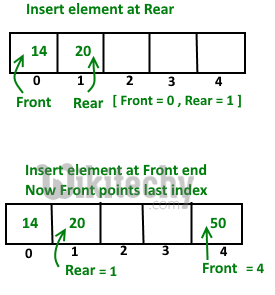
Insert Elements at Rear end

a). First we check dequeue if Full or Not 
b). IF Rear == Size-1 
       then reinitialize Rear = 0 ;
    Else increment Rear by '1'
    and push current key into Arr[ rear ] = key 
Front remain same.
[ad type=”banner”]

Insert Elements at Front end

a). First we check dequeue if Full or Not
b). IF Front == 0 || initial position, move Front
                     to points last index of array
       front = size - 1
    Else decremented front by '1' and push 
         current key into Arr[ Front] = key 
Rear remain same. 

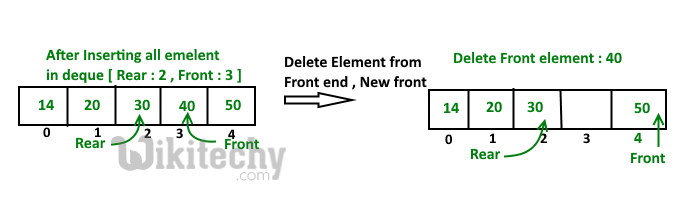
Implementation of Deque using circular array

Delete Element From Rear end

a). first Check dequeue is Empty or Not
b).  If dequeue has only one element
        front = -1 ; rear =-1 ;
    Else IF Rear points to the first index of array
         it's means we have to move rear to points 
         last index [ now first inserted element at 
         front end become rear end ]  
            rear = size-1 ;
    Else || decrease rear by '1'  
            rear = rear-1;
[ad type=”banner”]

Delete Element From Front end

a). first Check dequeue is Empty or Not
b).  If dequeue has only one element
            front = -1 ; rear =-1 ;
    Else IF front points to the last index of the array
         it's means we have no more elements in array so 
          we move front to points first index of array
            front = 0 ;
    Else || increment Front by '1'  
            front = front+1;
Implementation of Deque using -circular array

Java Implementation Dequeue Using Circular Array:

// Java implementation of De-queue using circular
// array
  
// A structure to represent a Deque
class Deque
{
    static final int MAX = 100;
    int  arr[];
    int  front;
    int  rear;
    int  size;
     
    public Deque(int size)
    {
        arr = new int[MAX];
        front = -1;
        rear = 0;
        this.size = size;
    }
  
    /*// Operations on Deque:
    void  insertfront(int key);
    void  insertrear(int key);
    void  deletefront();
    void  deleterear();
    bool  isFull();
    bool  isEmpty();
    int  getFront();
    int  getRear();*/
  
    // Checks whether Deque is full or not.
    boolean isFull()
    {
        return ((front == 0 && rear == size-1)||
            front == rear+1);
    }
  
    // Checks whether Deque is empty or not.
    boolean isEmpty ()
    {
        return (front == -1);
    }
  
    // Inserts an element at front
    void insertfront(int key)
    {
        // check whether Deque if  full or not
        if (isFull())
        {
            System.out.println("Overflow"); 
            return;
        }
  
        // If queue is initially empty
        if (front == -1)
        {
            front = 0;
            rear = 0;
        }
         
        // front is at first position of queue
        else if (front == 0)
            front = size - 1 ;
  
        else // decrement front end by '1'
            front = front-1;
  
        // insert current element into Deque
        arr[front] = key ;
    }
  
    // function to inset element at rear end
    // of Deque.
    void insertrear(int key)
    {
        if (isFull())
        {
            System.out.println(" Overflow ");
            return;
        }
  
        // If queue is initially empty
        if (front == -1)
        {
            front = 0;
            rear = 0;
        }
  
        // rear is at last position of queue
        else if (rear == size-1)
            rear = 0;
  
        // increment rear end by '1'
        else
            rear = rear+1;
         
        // insert current element into Deque
        arr[rear] = key ;
    }
  
    // Deletes element at front end of Deque
    void deletefront()
    {
        // check whether Deque is empty or not
        if (isEmpty())
        {
            System.out.println("Queue Underflow\n");
            return ;
        }
  
        // Deque has only one element
        if (front == rear)
        {
            front = -1;
            rear = -1;
        }
        else
            // back to initial position
            if (front == size -1)
                front = 0;
  
            else // increment front by '1' to remove current
                // front value from Deque
                front = front+1;
    }
  
    // Delete element at rear end of Deque
    void deleterear()
    {
        if (isEmpty())
        {
            System.out.println(" Underflow");
            return ;
        }
  
        // Deque has only one element
        if (front == rear)
        {
            front = -1;
            rear = -1;
        }
        else if (rear == 0)
            rear = size-1;
        else
            rear = rear-1;
    }
  
    // Returns front element of Deque
    int getFront()
    {
        // check whether Deque is empty or not
        if (isEmpty())
        {
            System.out.println(" Underflow");
            return -1 ;
        }
        return arr[front];
    }
  
    // function return rear element of Deque
    int getRear()
    {
        // check whether Deque is empty or not
        if(isEmpty() || rear < 0)
        {
            System.out.println(" Underflow\n");
            return -1 ;
        }
        return arr[rear];
    }
  
    // Driver program to test above function
    public static void main(String[] args)
    {
         
         Deque dq = new Deque(5);
          
         System.out.println("Insert element at rear end  : 5 ");
         dq.insertrear(5);
          
         System.out.println("insert element at rear end : 10 ");
         dq.insertrear(10);
          
         System.out.println("get rear element : "+ dq.getRear());
          
         dq.deleterear();
         System.out.println("After delete rear element new rear become : " + 
                                dq.getRear());
          
         System.out.println("inserting element at front end");
         dq.insertfront(15);
          
         System.out.println("get front element: " +dq.getFront());
          
         dq.deletefront();
          
         System.out.println("After delete front element new front become : " +
                                    +  dq.getFront());
         
    }
}

Output:

insert element at rear end  : 5
insert element at rear end : 10
get rear element : 10
After delete rear element new rear become : 5
inserting element at front end
get front element : 15
After delete front element new front become : 5

Time Complexity: Time complexity of all operations like insertfront(), insertlast(), deletefront(), deletelast() is O(1).

[ad type=”banner”]

Categorized in:

Data StructuresQueue

Tagged in:

, , , , , , ,