Inorder predecessor and successor for a given key in BST
Inorder predecessor and successor for a given key in BST
I recently encountered with a question in an interview at e-commerce company. The interviewer asked the following question:
There is BST given with root node with key part as integer only. The structure of each node is as follows:
You need to find the inorder successor and predecessor of a given key. In case the given key is not found in BST, then return the two values within which this key will lie.
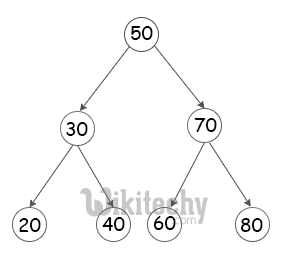
Following is the algorithm to reach the desired result. Its a recursive method:
Input: root node, key
output: predecessor node, successor node
1. If root is NULL
then return
2. if key is found then
a. If its left subtree is not null
Then predecessor will be the right most
child of left subtree or left child itself.
b. If its right subtree is not null
The successor will be the left most child
of right subtree or right child itself.
return
3. If key is smaller then root node
set the successor as root
search recursively into left subtree
else
set the predecessor as root
search recursively into right subtree
Implementation of Python code:
[ad type=”banner”]Output:
Predecessor is 60 Successor is 70