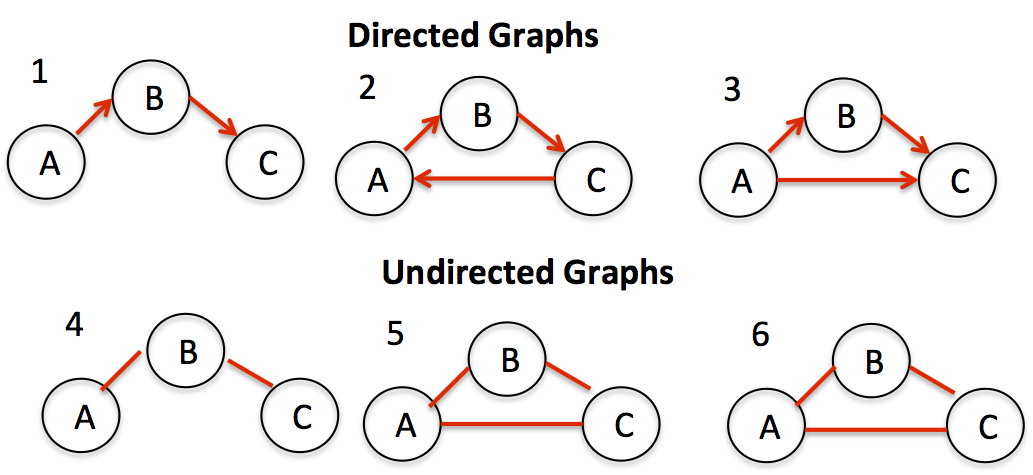
Find if there is a path between two vertices in a directed graph
Given a Directed Graph and two vertices in it, check whether there is a path from the first given vertex to second. For example, in the following graph, there is a path from vertex 1 to 3. As another example, there is no path from 3 to 0.
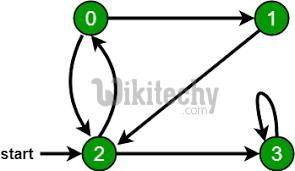
We can either use Breadth First Search (BFS) or Depth First Search (DFS) to find path between two vertices. Take the first vertex as source in BFS (or DFS), follow the standard BFS (or DFS). If we see the second vertex in our traversal, then return true. Else return false.
Following is Python code that use BFS for finding reachability of second vertex from first vertex.
Python Programming Find if there is a path between two vertices in a directed graph:
# program to check if there is exist a path between two vertices
# of a graph
from collections import defaultdict
#This class represents a directed graph using adjacency list representation
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = defaultdict(list) # default dictionary to store graph
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
# Use BFS to check path between s and d
def isReachable(self, s, d):
# Mark all the vertices as not visited
visited =[False]*(self.V)
# Create a queue for BFS
queue=[]
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
while queue:
#Dequeue a vertex from queue
n = queue.pop(0)
# If this adjacent node is the destination node,
# then return true
if n == d:
return True
# Else, continue to do BFS
for i in self.graph[n]:
if visited[i] == False:
queue.append(i)
visited[i] = True
# If BFS is complete without visited d
return False
# Create a graph given in the above diagram
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
u =1; v = 3
if g.isReachable(u, v):
print("There is a path from %d to %d" % (u,v))
else :
print("There is no path from %d to %d" % (u,v))
u = 3; v = 1
if g.isReachable(u, v) :
print("There is a path from %d to %d" % (u,v))
else :
print("There is no path from %d to %d" % (u,v))
Output:
There is a path from 1 to 3
There is no path from 3 to 1
[ad type=”banner”]