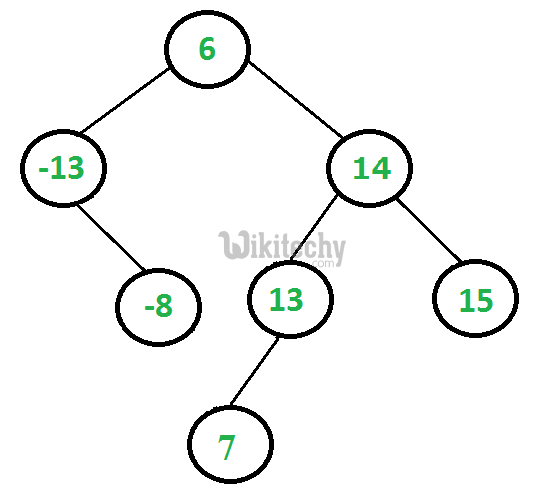
Python program to check if a binary tree is BST:

A binary search tree (BST) is a node based binary tree data structure which has the following properties.
• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

From the above properties it naturally follows that:
Each node (item in the tree) has a distinct key.

METHOD 1 (Correct and Efficient)

A better solution looks at each node only once. The trick is to write a utility helper function isBSTUtil(struct node* node, int min, int max) that traverses down the tree keeping track of the narrowing min and max allowed values as it goes, looking at each node only once. The initial values for min and max should be INT_MIN and INT_MAX — they narrow from there.

/* Returns true if the given tree is a binary search tree 
 (efficient version). */ 
int isBST(struct node* node) 
{ 
  return(isBSTUtil(node, INT_MIN, INT_MAX)); 
} 

/* Returns true if the given tree is a BST and its 
 values are >= min and <= max. */ 
int is BST Util(struct node* node, int min, int max)

Implementation of Python Program:

# Python program to check if a binary tree is bst or not
 
INT_MAX = 4294967296
INT_MIN = -4294967296
 
# A binary tree node
class Node:
 
    # Constructor to create a new node
    def __init__(self, data):
        self.data = data 
        self.left = None
        self.right = None
 
 
# Returns true if the given tree is a binary search tree
# (efficient version)
def isBST(node):
    return (isBSTUtil(node, INT_MIN, INT_MAX))
 
# Retusn true if the given tree is a BST and its values
# >= min and <= max
def isBSTUtil(node, mini, maxi):
     
    # An empty tree is BST
    if node is None:
        return True
 
    # False if this node violates min/max constraint
    if node.data < mini or node.data > maxi:
        return False
 
    # Otherwise check the subtrees recursively
    # tightening the min or max constraint
    return (isBSTUtil(node.left, mini, node.data -1) and
          isBSTUtil(node.right, node.data+1, maxi))
 
# Driver program to test above function
root = Node(4)
root.left = Node(2)
root.right = Node(5)
root.left.left = Node(1)
root.left.right = Node(3)
 
if (isBST(root)):
    print "Is BST"
else:
    print "Not a BST"
 
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

Output:

Is BST

Time Complexity: O(n) 
Auxiliary Space : O(1) if Function Call Stack size is not considered, otherwise O(n)