A triangulation of a convex polygon is formed by drawing diagonals between non-adjacent vertices (corners) such that the diagonals never intersect. The problem is to find the cost of triangulation with the minimum cost. The cost of a triangulation is sum of the weights of its component triangles. Weight of each triangle is its perimeter (sum of lengths of all sides)
See following example taken from this source.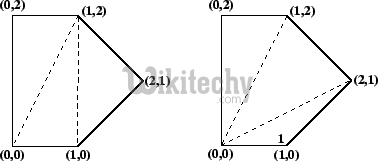
Two triangulations of the same convex pentagon. The triangulation on the left has a cost of 8 + 2√2 + 2√5 (approximately 15.30), the one on the right has a cost of 4 + 2√2 + 4√5 (approximately 15.77).
This problem has recursive substructure. The idea is to divide the polygon into three parts: a single triangle, the sub-polygon to the left, and the sub-polygon to the right. We try all possible divisions like this and find the one that minimizes the cost of the triangle plus the cost of the triangulation of the two sub-polygons.
Let Minimum Cost of triangulation of vertices from i to j be minCost(i, j)
If j <= i + 2 Then
minCost(i, j) = 0
Else
minCost(i, j) = Min { minCost(i, k) + minCost(k, j) + cost(i, k, j) }
Here k varies from 'i+1' to 'j-1'
Cost of a triangle formed by edges (i, j), (j, k) and (k, j) is
cost(i, j, k) = dist(i, j) + dist(j, k) + dist(k, j)
[ad type=”banner”]
Following is C++ implementation of above naive recursive formula.
C++
// Recursive implementation for minimum cost convex polygon triangulation
#include <iostream>
#include <cmath>
#define MAX 1000000.0
using namespace std;
// Structure of a point in 2D plane
struct Point
{
int x, y;
};
// Utility function to find minimum of two double values
double min(double x, double y)
{
return (x <= y)? x : y;
}
// A utility function to find distance between two points in a plane
double dist(Point p1, Point p2)
{
return sqrt((p1.x - p2.x)*(p1.x - p2.x) +
(p1.y - p2.y)*(p1.y - p2.y));
}
// A utility function to find cost of a triangle. The cost is considered
// as perimeter (sum of lengths of all edges) of the triangle
double cost(Point points[], int i, int j, int k)
{
Point p1 = points[i], p2 = points[j], p3 = points[k];
return dist(p1, p2) + dist(p2, p3) + dist(p3, p1);
}
// A recursive function to find minimum cost of polygon triangulation
// The polygon is represented by points[i..j].
double mTC(Point points[], int i, int j)
{
// There must be at least three points between i and j
// (including i and j)
if (j < i+2)
return 0;
// Initialize result as infinite
double res = MAX;
// Find minimum triangulation by considering all
for (int k=i+1; k<j; k++)
res = min(res, (mTC(points, i, k) + mTC(points, k, j) +
cost(points, i, k, j)));
return res;
}
// Driver program to test above functions
int main()
{
Point points[] = {{0, 0}, {1, 0}, {2, 1}, {1, 2}, {0, 2}};
int n = sizeof(points)/sizeof(points[0]);
cout << mTC(points, 0, n-1);
return 0;
}
Output:
15.3006
The above problem is similar to Matrix Chain Multiplication. The following is recursion tree for mTC(points[], 0, 4).
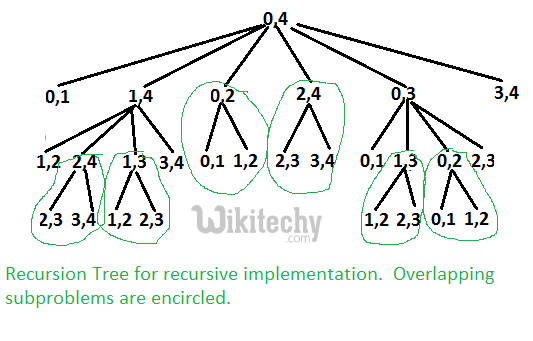
It can be easily seen in the above recursion tree that the problem has many overlapping subproblems. Since the problem has both properties: Optimal Substructure and Overlapping Subproblems, it can be efficiently solved using dynamic programming.
[ad type=”banner”]
Following is C++ implementation of dynamic programming solution.
C++
// A Dynamic Programming based program to find minimum cost of convex
// polygon triangulation
#include <iostream>
#include <cmath>
#define MAX 1000000.0
using namespace std;
// Structure of a point in 2D plane
struct Point
{
int x, y;
};
// Utility function to find minimum of two double values
double min(double x, double y)
{
return (x <= y)? x : y;
}
// A utility function to find distance between two points in a plane
double dist(Point p1, Point p2)
{
return sqrt((p1.x - p2.x)*(p1.x - p2.x) +
(p1.y - p2.y)*(p1.y - p2.y));
}
// A utility function to find cost of a triangle. The cost is considered
// as perimeter (sum of lengths of all edges) of the triangle
double cost(Point points[], int i, int j, int k)
{
Point p1 = points[i], p2 = points[j], p3 = points[k];
return dist(p1, p2) + dist(p2, p3) + dist(p3, p1);
}
// A Dynamic programming based function to find minimum cost for convex
// polygon triangulation.
double mTCDP(Point points[], int n)
{
// There must be at least 3 points to form a triangle
if (n < 3)
return 0;
// table to store results of subproblems. table[i][j] stores cost of
// triangulation of points from i to j. The entry table[0][n-1] stores
// the final result.
double table[n][n];
// Fill table using above recursive formula. Note that the table
// is filled in diagonal fashion i.e., from diagonal elements to
// table[0][n-1] which is the result.
for (int gap = 0; gap < n; gap++)
{
for (int i = 0, j = gap; j < n; i++, j++)
{
if (j < i+2)
table[i][j] = 0.0;
else
{
table[i][j] = MAX;
for (int k = i+1; k < j; k++)
{
double val = table[i][k] + table[k][j] + cost(points,i,j,k);
if (table[i][j] > val)
table[i][j] = val;
}
}
}
}
return table[0][n-1];
}
// Driver program to test above functions
int main()
{
Point points[] = {{0, 0}, {1, 0}, {2, 1}, {1, 2}, {0, 2}};
int n = sizeof(points)/sizeof(points[0]);
cout << mTCDP(points, n);
return 0;
}
Output:
15.3006
Time complexity of the above dynamic programming solution is O(n3).
[ad type=”banner”]