Maximum Sum Increasing Subsequence

Given an array of n positive integers. Write a program to find the sum of maximum sum subsequence of the given array such that the integers in the subsequence are sorted in increasing order.

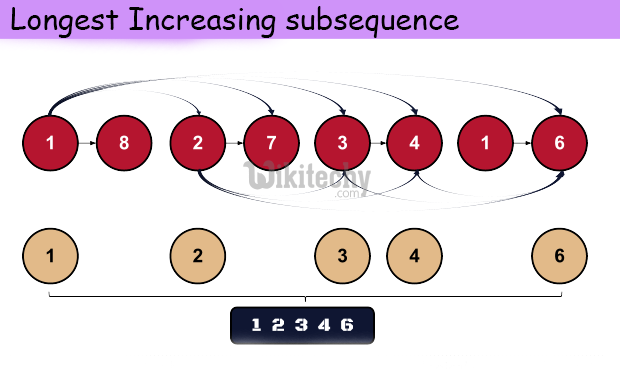
For example, if input is {1, 101, 2, 3, 100, 4, 5}, then output should be 106 (1 + 2 + 3 + 100), if the input array is {3, 4, 5, 10}, then output should be 22 (3 + 4 + 5 + 10) and if the input array is {10, 5, 4, 3}, then output should be 10

Solution:

This problem is a variation of standard Longest Increasing Subsequence (LIS) problem. We need a slight change in the Dynamic Programming solution of LIS problem. All we need to change is to use sum as a criteria instead of length of increasing subsequence.

Java implementation:

[pastacode lang=”java” manual=”class%20MSIS%0A%7B%0A%0A%20%20%0A%20%20%20%20static%20int%20maxSumIS(%20int%20arr%5B%5D%2C%20int%20n%20)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20int%20i%2C%20j%2C%20max%20%3D%200%3B%0A%20%20%20%20%20%20%20%20int%20msis%5B%5D%20%3D%20new%20int%5Bn%5D%3B%0A%20%0A%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20for%20(%20i%20%3D%200%3B%20i%20%3C%20n%3B%20i%2B%2B%20)%0A%20%20%20%20%20%20%20%20%20%20%20%20msis%5Bi%5D%20%3D%20arr%5Bi%5D%3B%0A%20%0A%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20for%20(%20i%20%3D%201%3B%20i%20%3C%20n%3B%20i%2B%2B%20)%0A%20%20%20%20%20%20%20%20%20%20%20%20for%20(%20j%20%3D%200%3B%20j%20%3C%20i%3B%20j%2B%2B%20)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(%20arr%5Bi%5D%20%3E%20arr%5Bj%5D%20%26%26%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20msis%5Bi%5D%20%3C%20msis%5Bj%5D%20%2B%20arr%5Bi%5D)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20msis%5Bi%5D%20%3D%20msis%5Bj%5D%20%2B%20arr%5Bi%5D%3B%0A%20%0A%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20for%20(%20i%20%3D%200%3B%20i%20%3C%20n%3B%20i%2B%2B%20)%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20(%20max%20%3C%20msis%5Bi%5D%20)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20max%20%3D%20msis%5Bi%5D%3B%0A%20%0A%20%20%20%20%20%20%20%20return%20max%3B%0A%20%20%20%20%7D%0A%20%0A%0A%20%20%20%20public%20static%20void%20main(String%20args%5B%5D)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20int%20arr%5B%5D%20%3D%20new%20int%5B%5D%7B1%2C%20101%2C%202%2C%203%2C%20100%2C%204%2C%205%7D%3B%0A%20%20%20%20%20%20%20%20int%20n%20%3D%20arr.length%3B%0A%20%20%20%20%20%20%20%20System.out.println(%22Sum%20of%20maximum%20sum%20increasing%20%22%2B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%22%20subsequence%20is%20%22%2B%0A%20%20%20%20%20%20%20%20maxSumIS(%20arr%2C%20n%20)%20)%3B%0A%20%20%20%20%7D%0A%7D” message=”Java” highlight=”” provider=”manual”/]

Output:

Sum of maximum sum increasing subsequence is 106

Time Complexity: O(n^2)

[ad type=”banner”]