Write an efficient Java program to find the sum of contiguous subarray within a one-dimensional array of numbers which has the largest sum.

Kadane’s Algorithm:

Initialize:
    max_so_far = 0
    max_ending_here = 0

Loop for each element of the array
  (a) max_ending_here = max_ending_here + a[i]
  (b) if(max_ending_here < 0)
            max_ending_here = 0
  (c) if(max_so_far < max_ending_here)
            max_so_far = max_ending_here
return max_so_far

Explanation:
Simple idea of the Kadane’s algorithm is to look for all positive contiguous segments of the array (max_ending_here is used for this). And keep track of maximum sum contiguous segment among all positive segments (max_so_far is used for this). Each time we get a positive sum compare it with max_so_far and update max_so_far if it is greater than max_so_far

    Lets take the example:
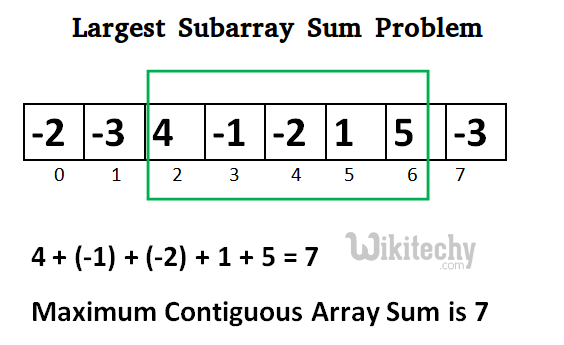
    {-2, -3, 4, -1, -2, 1, 5, -3}

    max_so_far = max_ending_here = 0

    for i=0,  a[0] =  -2
    max_ending_here = max_ending_here + (-2)
    Set max_ending_here = 0 because max_ending_here < 0

    for i=1,  a[1] =  -3
    max_ending_here = max_ending_here + (-3)
    Set max_ending_here = 0 because max_ending_here < 0

    for i=2,  a[2] =  4
    max_ending_here = max_ending_here + (4)
    max_ending_here = 4
    max_so_far is updated to 4 because max_ending_here greater 
    than max_so_far which was 0 till now

    for i=3,  a[3] =  -1
    max_ending_here = max_ending_here + (-1)
    max_ending_here = 3

    for i=4,  a[4] =  -2
    max_ending_here = max_ending_here + (-2)
    max_ending_here = 1

    for i=5,  a[5] =  1
    max_ending_here = max_ending_here + (1)
    max_ending_here = 2

    for i=6,  a[6] =  5
    max_ending_here = max_ending_here + (5)
    max_ending_here = 7
    max_so_far is updated to 7 because max_ending_here is 
    greater than max_so_far

    for i=7,  a[7] =  -3
    max_ending_here = max_ending_here + (-3)
    max_ending_here = 4

Program:

Maximum contiguous sum is 7

import java.io.*;
// Java program to print largest contiguous array sum
import java.util.*;
 
class Kadane
{
    public static void main (String[] args)
    {
        int [] a = {-2, -3, 4, -1, -2, 1, 5, -3};
        System.out.println("Maximum contiguous sum is " +
                                       maxSubArraySum(a));
    }
 
    static int maxSubArraySum(int a[])
    {
        int size = a.length;
        int max_so_far = Integer.MIN_VALUE, max_ending_here = 0;
 
        for (int i = 0; i < size; i++)
        {
            max_ending_here = max_ending_here + a[i];
            if (max_so_far < max_ending_here)
                max_so_far = max_ending_here;
            if (max_ending_here < 0)
                max_ending_here = 0;
        }
        return max_so_far;
    }
}