[
[ Solved -11 Answers] JAVA – Why is it faster to process a sorted array than an unsorted array
A piece of C++ code that seems very peculiar. For some reason, sorting the data miraculously makes the code almost six times faster.
[pastacode lang=”cpp” manual=”%23include%20%3Calgorithm%3E%0A%23include%20%3Cctime%3E%0A%23include%20%3Ciostream%3E%0A%0Aint%20main()%0A%7B%0A%20%20%20%20%2F%2F%20Generate%20data%0A%20%20%20%20const%20unsigned%20arraySize%20%3D%2032768%3B%0A%20%20%20%20int%20data%5BarraySize%5D%3B%0A%0A%20%20%20%20for%20(unsigned%20c%20%3D%200%3B%20c%20%3C%20arraySize%3B%20%2B%2Bc)%0A%20%20%20%20%20%20%20%20data%5Bc%5D%20%3D%20std%3A%3Arand()%20%25%20256%3B%0A%0A%20%20%20%20%2F%2F%20!!!%20With%20this%2C%20the%20next%20loop%20runs%20faster%0A%20%20%20%20std%3A%3Asort(data%2C%20data%20%2B%20arraySize)%3B%0A%2F%2F%20Test%0A%20%20%20%20clock_t%20start%20%3D%20clock()%3B%0A%20%20%20%20long%20long%20sum%20%3D%200%3B%0A%20for%20(unsigned%20i%20%3D%200%3B%20i%20%3C%20100000%3B%20%2B%2Bi)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20Primary%20loop%0A%20%20%20%20%20%20%20%20for%20(unsigned%20c%20%3D%200%3B%20c%20%3C%20arraySize%3B%20%2B%2Bc)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20(data%5Bc%5D%20%3E%3D%20128)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sum%20%2B%3D%20data%5Bc%5D%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%7D%0A%20double%20elapsedTime%20%3D%20static_cast%3Cdouble%3E(clock()%20-%20start)%20%2F%20CLOCKS_PER_SEC%3B%0A%20std%3A%3Acout%20%3C%3C%20elapsedTime%20%3C%3C%20std%3A%3Aendl%3B%0A%20std%3A%3Acout%20%3C%3C%20%22sum%20%3D%20%22%20%3C%3C%20sum%20%3C%3C%20std%3A%3Aendl%3B%0A%7D%0A” message=”c++ code” highlight=”” provider=”manual”/]- Without std::sort(data, data + arraySize);, the code runs in 11.54 seconds.
- With the sorted data, the code runs in 1.93 seconds.
Initially, this might be just a language or compiler anomaly. So a Trail in Java.
[pastacode lang=”java” manual=”import%20java.util.Arrays%3B%0Aimport%20java.util.Random%3B%0A%0Apublic%20class%20Main%0A%7B%0A%20%20%20%20public%20static%20void%20main(String%5B%5D%20args)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20Generate%20data%0A%20%20%20%20%20%20%20%20int%20arraySize%20%3D%2032768%3B%0A%20%20%20%20%20%20%20%20int%20data%5B%5D%20%3D%20new%20int%5BarraySize%5D%3B%0A%0A%20%20%20%20%20%20%20%20Random%20rnd%20%3D%20new%20Random(0)%3B%0A%20%20%20%20%20%20%20%20for%20(int%20c%20%3D%200%3B%20c%20%3C%20arraySize%3B%20%2B%2Bc)%0A%20%20%20%20%20%20%20%20%20%20%20%20data%5Bc%5D%20%3D%20rnd.nextInt()%20%25%20256%3B%0A%0A%20%20%20%20%20%20%20%20%2F%2F%20!!!%20With%20this%2C%20the%20next%20loop%20runs%20faster%0A%20%20%20%20%20%20%20%20Arrays.sort(data)%3B%0A%2F%2F%20Test%0A%20%20%20%20%20%20%20%20long%20start%20%3D%20System.nanoTime()%3B%0A%20%20%20%20%20%20%20%20long%20sum%20%3D%200%3B%0A%0A%20%20%20%20%20%20%20%20for%20(int%20i%20%3D%200%3B%20i%20%3C%20100000%3B%20%2B%2Bi)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20Primary%20loop%0A%20%20%20%20%20%20%20%20%20%20%20%20for%20(int%20c%20%3D%200%3B%20c%20%3C%20arraySize%3B%20%2B%2Bc)%0A%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(data%5Bc%5D%20%3E%3D%20128)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sum%20%2B%3D%20data%5Bc%5D%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%7D%0A%0A%20%20%20%20%20%20%20%20System.out.println((System.nanoTime()%20-%20start)%20%2F%201000000000.0)%3B%0A%20%20%20%20%20%20%20%20System.out.println(%22sum%20%3D%20%22%20%2B%20sum)%3B%0A%20%20%20%20%7D%0A%7D%0A” message=”java code” highlight=”” provider=”manual”/]With a somewhat similar but less extreme result.
[pastacode lang=”cpp” manual=”if%20(data%5Bc%5D%20%3E%3D%20128)%20sum%20%2B%3D%20data%5Bc%5D%3B” message=”c ++ code” highlight=”” provider=”manual”/]- Notice that the data is evenly distributed between 0 and 255.
- When the data is sorted, roughly the first half of the iterations will not enter the if-statement.
- After that, they will all enter the if-statement.
- This is very friendly to the branch predictor since the branch consecutively goes the same direction many times.
- Even a simple saturating counter will correctly predict the branch except for the few iterations after it switches direction.
Quick visualization:
T = branch taken N = branch not taken data[] = 0, 1, 2, 3, 4, … 126, 127, 128, 129, 130, … 250, 251, 252, … branch = N N N N N … N N T T T … T T T … = NNNNNNNNNNNN … NNNNNNNTTTTTTTTT … TTTTTTTTTT (easy to predict)
- However, when the data is completely random, the branch predictor is rendered useless because it can’t predict random data.
data[] = 226, 185, 125, 158, 198, 144, 217, 79, 202, 118, 14, 150, 177, 182, 133, … branch = T, T, N, T, T, T, T, N, T, N, N, T, T, T, N … = TTNTTTTNTNNTTTN … (completely random – hard to predict)
If the compiler isn’t able to optimize the branch into a conditional move,
Replace:
[pastacode lang=”cpp” manual=”if%20(data%5Bc%5D%20%3E%3D%20128)%20%0Asum%20%2B%3D%20data%5Bc%5D%3B%20%0A” message=”c++ code” highlight=”” provider=”manual”/]with:
[pastacode lang=”cpp” manual=”int%20t%20%3D%20(data%5Bc%5D%20-%20128)%20%3E%3E%2031%3B%0Asum%20%2B%3D%20~t%20%26%20data%5Bc%5D%3B%20%0A” message=”c++ code” highlight=”” provider=”manual”/]- This eliminates the branch and replaces it with some bitwise operations.
C++ – Visual Studio 2010 – x64 Release
[pastacode lang=”cpp” manual=”%2F%2F%20Branch%20-%20Random%20%0Aseconds%20%3D%2011.777%20%0A%2F%2F%20Branch%20-%20Sorted%20%0Aseconds%20%3D%202.352%20%0A%2F%2F%20Branchless%20-%20Random%20%0Aseconds%20%3D%202.564%20%0A%2F%2F%20Branchless%20%E2%80%93%20Sorted%0Aseconds%20%3D%202.587%20%0A” message=”c ++ code” highlight=”” provider=”manual”/]Java – Netbeans 7.1.1 JDK 7 – x64
[pastacode lang=”java” manual=”%2F%2F%20Branch%20-%20Random%20%0Aseconds%20%3D%2010.93293813%20%0A%2F%2F%20Branch%20-%20Sorted%20%0Aseconds%20%3D%205.643797077%20%0A%2F%2F%20Branchless%20%E2%80%93%20Random%0A%20seconds%20%3D%203.113581453%20%0A%2F%2F%20Branchless%20%E2%80%93%20Sorted%0A%20seconds%20%3D%203.186068823%20%0A” message=”java code” highlight=”” provider=”manual”/]- With the Branch:There is a huge difference between the sorted and unsorted data.
- With the Hack:There is no difference between sorted and unsorted data.
- In the C++ case, the hack is actually a tad slower than with the branch when the data is sorted.
- The meaning of this particular if… else… branch is to add something when a condition is satisfied.
- This type of branch can be easily transformed into a conditional movestatement, which would be compiled into a conditional move instruction: cmovl, in an x86 system.
- The branch and thus the potential branch prediction penalty is removed.
- In C, thus C++, the statement, which would compile directly (without any optimization) into the conditional move instruction in x86, is the ternary operator … ? … : ….
- So it can be rewritten as:
Thus from the previous fix, lets investigate the x86 assembly they generate. For simplicity, we use two functions max1 and max2.
[pastacode lang=”java” manual=”max1%C2%A0uses%20the%20conditional%20branch%C2%A0if…%20else%20…%3A%0Aint%20max1(int%20a%2C%20int%20b)%20%0A%7B%20%0Aif%20(a%20%3E%20b)%0A%20return%20a%3B%0A%20else%20return%20b%3B%20%0A%7D%20%0A” message=”java code” highlight=”” provider=”manual”/] [pastacode lang=”java” manual=”max2%C2%A0uses%20the%20ternary%20operator%C2%A0…%20%3F%20…%20%3A%20…%3A%0Aint%20max2(int%20a%2C%20int%20b)%0A%20%7B%20%0Areturn%20a%20%3E%20b%20%3F%20a%20%3A%20b%3B%20%0A%7D%20%0A” message=”java code” highlight=”” provider=”manual”/] [pastacode lang=”cpp” manual=”max1%20%0Amovl%20%25edi%2C%20-4(%25rbp)%20%0Amovl%20%25esi%2C%20-8(%25rbp)%20%0Amovl%20-4(%25rbp)%2C%20%25eax%20%0Acmpl%20-8(%25rbp)%2C%20%25eax%20%0Ajle%20.L2%20%0Amovl%20-4(%25rbp)%2C%20%25eax%20%0Amovl%20%25eax%2C%20-12(%25rbp)%20%0Ajmp%20.L4%20%0A.L2%3A%20%0Amovl%20-8(%25rbp)%2C%20%25eax%20%0Amovl%20%25eax%2C%20-12(%25rbp)%20%0A.L4%3A%20%0Amovl%20-12(%25rbp)%2C%20%25eax%20%0Aleave%20%0Aret%20%0A%3Amax2%20%0Amovl%20%25edi%2C%20-4(%25rbp)%20%0Amovl%20%25esi%2C%20-8(%25rbp)%20%0Amovl%20-4(%25rbp)%2C%20%25eax%20%0Acmpl%20%25eax%2C%20-8(%25rbp)%20%0Acmovge%20-8(%25rbp)%2C%20%25eax%20%0Aleave%20%0Aret%20%0A” message=”C++ code” highlight=”” provider=”manual”/]- max2 uses much less code due to the usage of instruction cmovge
- But the real gain is that max2does not involve branch jumps, jmp, which would have a significant performance penalty if the predicted result is not right
- In a typical x86 processor, the execution of an instruction is divided into several stages.
- Thus they have different hardware to deal with different stages.
- So we do not have to wait for one instruction to finish to start a new one.
- This is called pipelining.
Starting with the original loop:
[pastacode lang=”java” manual=”for%20(unsigned%20i%20%3D%200%3B%20i%20%3C%20100000%3B%20%2B%2Bi)%0A%20%7B%20%0Afor%20(unsigned%20j%20%3D%200%3B%20j%20%3C%20arraySize%3B%20%2B%2Bj)%0A%20%7B%20%0Aif%20(data%5Bj%5D%20%3E%3D%20128)%0A%20sum%20%2B%3D%20data%5Bj%5D%3B%20%0A%7D%20%0A%7D%20%0A” message=”java code” highlight=”” provider=”manual”/]With loop interchange, we can change this loop to:
[pastacode lang=”java” manual=”for%20(unsigned%20j%20%3D%200%3B%20j%20%3C%20arraySize%3B%20%2B%2Bj)%20%0A%7B%20%0Afor%20(unsigned%20i%20%3D%200%3B%20i%20%3C%20100000%3B%20%2B%2Bi)%0A%20%7B%20%0Aif%20(data%5Bj%5D%20%3E%3D%20128)%0A%20sum%20%2B%3D%20data%5Bj%5D%3B%20%0A%7D%20%0A%7D%20%0A” message=”java code” highlight=”” provider=”manual”/]if” conditional is constant throughout the execution of the “i” loop, so you can hoist the “if” out:
[pastacode lang=”java” manual=”for%20(unsigned%20j%20%3D%200%3B%20j%20%3C%20arraySize%3B%20%2B%2Bj)%20%0A%7B%20%0Aif%20(data%5Bj%5D%20%3E%3D%20128)%20%0A%7B%20%0Afor%20(unsigned%20i%20%3D%200%3B%20i%20%3C%20100000%3B%20%2B%2Bi)%20%0A%7B%20%0Asum%20%2B%3D%20data%5Bj%5D%3B%20%0A%7D%20%7D%20%7D%20%0A” message=”java code” highlight=”” provider=”manual”/]the inner loop can be collapsed into one single expression, assuming the floating point model allows it
[pastacode lang=”java” manual=”for%20(unsigned%20j%20%3D%200%3B%20j%20%3C%20arraySize%3B%20%2B%2Bj)%0A%20%7B%20%0Aif%20(data%5Bj%5D%20%3E%3D%20128)%0A%20%7B%20%0Asum%20%2B%3D%20data%5Bj%5D%20*%20100000%3B%0A%20%7D%20%0A%7D%20%0A” message=”java code” highlight=”” provider=”manual”/]- The Valgrind tool cachegrind has a branch-predictor simulator, enabled by using the –branch-sim=yes flag.
- Running it over the examples in this question, with the number of outer loops reduced to 10000 and compiled with g++, gives these results:
Sorted:
[pastacode lang=”java” manual=”%3D%3D32551%3D%3D%20Branches%3A%20%20%20%20%20%20%20%20656%2C645%2C130%20%20(%20%20656%2C609%2C208%20cond%20%2B%20%20%20%2035%2C922%20ind)%0A%3D%3D32551%3D%3D%20Mispredicts%3A%20%20%20%20%20%20%20%20%20169%2C556%20%20(%20%20%20%20%20%20169%2C095%20cond%20%2B%20%20%20%20%20%20%20461%20ind)%0A%3D%3D32551%3D%3D%20Mispred%20rate%3A%20%20%20%20%20%20%20%20%20%20%20%200.0%25%20(%20%20%20%20%20%20%20%20%20%200.0%25%20%20%20%20%20%2B%20%20%20%20%20%20%201.2%25%20%20%20)%0A” message=”java code” highlight=”” provider=”manual”/]Unsorted:
[pastacode lang=”java” manual=”%3D%3D32555%3D%3D%20Branches%3A%20%20%20%20%20%20%20%20655%2C996%2C082%20%20(%20%20655%2C960%2C160%20cond%20%2B%20%2035%2C922%20ind)%0A%3D%3D32555%3D%3D%20Mispredicts%3A%20%20%20%20%20164%2C073%2C152%20%20(%20%20164%2C072%2C692%20cond%20%2B%20%20%20%20%20460%20ind)%0A%3D%3D32555%3D%3D%20Mispred%20rate%3A%20%20%20%20%20%20%20%20%20%20%2025.0%25%20(%20%20%20%20%20%20%20%20%2025.0%25%20%20%20%20%20%2B%20%20%20%20%201.2%25%20%20%20)%0A” message=”java code” highlight=”” provider=”manual”/]- Drilling down into the line-by-line output produced by cg_annotate we see for the loop in question:
Sorted:
[pastacode lang=”java” manual=”Bc%20%20%20%20Bcm%20Bi%20Bim%0A%20%20%20%20%20%2010%2C001%20%20%20%20%20%204%20%200%20%20%200%20%20%20%20%20%20for%20(unsigned%20i%20%3D%200%3B%20i%20%3C%2010000%3B%20%2B%2Bi)%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%09%09%09%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%20%20%20%09%09%09%20%20%2F%2F%20primary%20loop%0A%20327%2C690%2C000%2010%2C016%20%200%20%20%200%20%20%20%20%20%20%20%20%20%20for%20(unsigned%20c%20%3D%200%3B%20c%20%3C%20%09%09%09%09arraySize%3B%20%2B%2Bc)%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%20%20%20%09%09%09%20%20%7B%0A%20327%2C680%2C000%2010%2C006%20%200%20%20%200%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(data%5Bc%5D%20%3E%3D%20128)%0A%20%20%20%20%20%20%20%20%20%20%200%20%20%20%20%20%200%20%200%20%20%200%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sum%20%2B%3D%20data%5Bc%5D%3B%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%20%20%20%20%09%09%20%7D%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%09%09%09%20%7D%0A” message=”java code” highlight=”” provider=”manual”/]Unsorted:
[pastacode lang=”java” manual=”%0A%20%20%20%20%20%20%20%20%20%20Bc%20%20%20%20%20%20%20%20%20Bcm%20Bi%20Bim%0A%20%20%20%20%20%2010%2C001%20%20%20%20%20%20%20%20%20%20%204%20%200%20%20%200%20%20%20%20%20%20for%20(unsigned%20i%20%3D%200%3B%20i%20%3C%2010000%3B%20%2B%2Bi)%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%09%09%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%20%20%20%20%09%09%20%2F%2F%20primary%20loop%0A%20327%2C690%2C000%20%20%20%20%20%2010%2C038%20%200%20%20%200%20%20%20%20%20%20%20%20%20%20for%20(unsigned%20c%20%3D%200%3B%20c%20%3C%20%09%09%09%09%09arraySize%3B%20%2B%2Bc)%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%20%20%20%09%09%20%20%7B%0A%20327%2C680%2C000%20164%2C050%2C007%20%200%20%20%200%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(data%5Bc%5D%20%3E%3D%20128)%0A%20%20%20%20%20%20%20%20%20%20%200%20%20%20%20%20%20%20%20%20%20%200%20%200%20%20%200%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%09sum%20%2B%3D%20data%5Bc%5D%3B%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%20%20%20%20%09%09%20%7D%0A%20%20%20%20%20%20%20%20%20%20%20.%20%20%20%20%20%20%20%20%20%20%20.%20%20.%20%20%20.%20%20%20%20%20%09%09%20%7D%0A” message=”java code” highlight=”” provider=”manual”/] [ad type=”banner”]- the problematic line – in the unsorted version the if (data[c] >= 128) line is causing 164,050,007 mispredicted conditional branches (Bcm) under cachegrind’s branch-predictor model, whereas it’s only causing 10,006 in the sorted version.
- On Linux you can use the performance counters subsystem to accomplish The Valgrind tool cachegrind has a branch-predictor simulator, enabled by using the –branch-sim=yes flag, but with native performance using CPU counters.
Sorted:
[pastacode lang=”java” manual=”Performance%20counter%20stats%20for%20′.%2Fsumtest_sorted’%3A%20%0A11808.095776%20task-clock%20%23%200.998%20CPUs%20utilized%20%0A1%2C062%20context-switches%20%23%200.090%20K%2Fsec%20%0A14%20CPU-migrations%20%23%200.001%20K%2Fsec%20%0A337%20page-faults%20%23%200.029%20K%2Fsec%20%0A26%2C487%2C882%2C764%20cycles%20%23%202.243%20GHz%20%0A41%2C025%2C654%2C322%20instructions%20%23%201.55%20insns%20per%20cycle%206%2C558%2C871%2C379%20branches%20%23%20555.455%20M%2Fsec%20%0A567%2C204%20branch-misses%20%23%200.01%25%20of%20all%20branches%2011.827228330%20seconds%20time%20elapsed%20%0A” message=”java code” highlight=”” provider=”manual”/]Unsorted:
[pastacode lang=”java” manual=”Performance%20counter%20stats%20for%20′.%2Fsumtest_unsorted’%3A%2028877.954344%20task-clock%20%23%200.998%20CPUs%20utilized%0A%202%2C584%20context-switches%20%23%200.089%20K%2Fsec%0A%2018%20CPU-migrations%20%23%200.001%20K%2Fsec%20%0A335%20page-faults%20%23%200.012%20K%2Fsec%20%0A65%2C076%2C127%2C595%20cycles%20%23%202.253%20GHz%20%0A41%2C032%2C528%2C741%20instructions%20%23%200.63%20insns%20per%20cycle%206%2C560%2C579%2C013%20branches%20%23%20227.183%20M%2Fsec%0A%201%2C646%2C394%2C749%20branch-misses%20%23%2025.10%25%20of%20all%20branches%2028.935500947%20seconds%20time%20elapsed%20%0A” message=”java code” highlight=”” provider=”manual”/]- It can also do source code annotation with dissassembly.
- perf record -e branch-misses ./sumtest_unsorted
- perf annotate -d sumtest_unsorted
Percent | Source code & Disassembly of sumtest_unsorted
[pastacode lang=”java” manual=”…%0A%20%20%20%20%20%20%20%20%20%3A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sum%20%2B%3D%20data%5Bc%5D%3B%0A%20%20%20%200.00%20%3A%20%20%20%20%20%20%20%20400a1a%3A%20%20%20%20%20%20%20mov%20%20%20%20-0x14(%25rbp)%2C%25eax%0A%20%20%2039.97%20%3A%20%20%20%20%20%20%20%20400a1d%3A%20%20%20%20%20%20%20mov%20%20%20%20%25eax%2C%25eax%0A%20%20%20%205.31%20%3A%20%20%20%20%20%20%20%20400a1f%3A%20%20%20%20%20%20%20mov%20%20%20%20-0x20040(%25rbp%2C%25rax%2C4)%2C%25eax%0A%20%20%20%204.60%20%3A%20%20%20%20%20%20%20%20400a26%3A%20%20%20%20%20%20%20cltq%20%20%20%0A%20%20%20%200.00%20%3A%20%20%20%20%20%20%20%20400a28%3A%20%20%20%20%20%20%20add%20%20%20%20%25rax%2C-0x30(%25rbp)%0A…%0A” message=”java code” highlight=”” provider=”manual”/]A common way to eliminate branch prediction is that, to work in managed languages -a table lookup instead of using a branch
[pastacode lang=”java” manual=”%2F%2F%20generate%20data%0Aint%20arraySize%20%3D%2032768%3B%0Aint%5B%5D%20data%20%3D%20new%20int%5BarraySize%5D%3B%0A%0ARandom%20rnd%20%3D%20new%20Random(0)%3B%0Afor%20(int%20c%20%3D%200%3B%20c%20%3C%20arraySize%3B%20%2B%2Bc)%0A%20%20%20%20data%5Bc%5D%20%3D%20rnd.Next(256)%3B%0A%0A%2F%2F%20Too%20keep%20the%20spirit%20of%20the%20code%20in-tact%20we%20will%20make%20a%20separate%20lookup%20table%0A%2F%2F%20(Assume%20we%20cannot%20modify%20’data’%20or%20the%20number%20of%20loops)%0Aint%5B%5D%20lookup%20%3D%20new%20int%5B256%5D%3B%0A%0Afor%20(int%20c%20%3D%200%3B%20c%20%3C%20256%3B%20%2B%2Bc)%0A%20%20%20%20lookup%5Bc%5D%20%3D%20(c%20%3E%3D%20128)%20%3F%20c%20%3A%200%3B%0A%2F%2F%20test%0ADateTime%20startTime%20%3D%20System.DateTime.Now%3B%0Along%20sum%20%3D%200%3B%0A%0Afor%20(int%20i%20%3D%200%3B%20i%20%3C%20100000%3B%20%2B%2Bi)%0A%7B%0A%20%20%20%20%2F%2F%20primary%20loop%0A%20%20%20%20for%20(int%20j%20%3D%200%3B%20j%20%3C%20arraySize%3B%20%2B%2Bj)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20here%20you%20basically%20want%20to%20use%20simple%20operations%20-%20so%20no%20%0A%20%20%20%20%20%20%20%20%2F%2F%20random%20branches%2C%20but%20things%20like%20%26%2C%20%7C%2C%20*%2C%20-%2C%20%2B%2C%20etc%20are%20fine.%0A%20%20%20%20%20%20%20%20sum%20%2B%3D%20lookup%5Bdata%5Bj%5D%5D%3B%0A%20%20%20%20%7D%0A%7D%0A%0ADateTime%20endTime%20%3D%20System.DateTime.Now%3B%0AConsole.WriteLine(endTime%20-%20startTime)%3B%0AConsole.WriteLine(%22sum%20%3D%20%22%20%2B%20sum)%3B%0A%0AConsole.ReadLine()%3B%0A” message=”java code” highlight=”” provider=”manual”/]- measure the performance of this loop with different conditions:
Here are the timings of the loop with different True-False patterns:
Condition Pattern Time (ms)
(i & 0×80000000) == 0 T repeated 322
(i & 0xffffffff) == 0 F repeated 276
(i & 1) == 0 TF alternating 760
(i & 3) == 0 TFFFTFFF… 513
(i & 2) == 0 TTFFTTFF… 1675
(i & 4) == 0 TTTTFFFFTTTTFFFF1275
(i & 8) == 0 8T 8F 8T 8F … 752
(i & 16) == 0 16T 16F 16T 16F … 490
- A “bad” true-false pattern can make an if-statement up to six times slower than a “good” pattern!
- Thus which pattern is good and which is bad depends on the exact instructions generated by the compiler and on the specific processor.
- The way to avoid branch prediction errors is to build a lookup table, and index it using the data
- By using the 0/1 value of the decision bit as an index into an array, we can make code that will be equally fast whether the data is sorted or not sorted.
- Our code will always add a value, but when the decision bit is 0, we will add the value somewhere we don’t care
This code wastes half of the adds, but never has a branch prediction failure.
- The technique of indexing into an array, instead of using an if statement, can be used for deciding which pointer to use.
- A library that implemented binary trees, and instead of having two named pointers (pLeft and pRight or whatever) had a length-2 array of pointers, and used the “decision bit” technique to decide which one to follow.
- For example, instead of:
- In the sorted case, you can do better than relying on successful branch prediction or any branchless comparison trick: completely remove the branch.
- The array is partitioned in a contiguous zone with data < 128 and another with data >= 128. So you should find the partition point with a dichotomic search (using Lg(arraySize) = 15 comparisons), then do a straight accumulation from that point.
Something like (unchecked)
[pastacode lang=”java” manual=”int%20i%3D%200%2C%20j%2C%20k%3D%20arraySize%3B%0Awhile%20(i%20%3C%20k)%0A%7B%0A%20%20j%3D%20(i%20%2B%20k)%20%3E%3E%201%3B%0A%20%20if%20(data%5Bj%5D%20%3E%3D%20128)%0A%20%20%20%20k%3D%20j%3B%0A%20%20else%0A%20%20%20%20i%3D%20j%3B%0A%7D%0Asum%3D%200%3B%0Afor%20(%3B%20i%20%3C%20arraySize%3B%20i%2B%2B)%0A%20%20sum%2B%3D%20data%5Bi%5D%3B%0A” message=”java code” highlight=”” provider=”manual”/]slightly more obfuscated
[pastacode lang=”java” manual=”int%20i%2C%20k%2C%20j%3D%20(i%20%2B%20k)%20%3E%3E%201%3B%0Afor%20(i%3D%200%2C%20k%3D%20arraySize%3B%20i%20%3C%20k%3B%20(data%5Bj%5D%20%3E%3D%20128%20%3F%20k%20%3A%20i)%3D%20j)%0A%20%20j%3D%20(i%20%2B%20k)%20%3E%3E%201%3B%0Afor%20(sum%3D%200%3B%20i%20%3C%20arraySize%3B%20i%2B%2B)%0A%20%20sum%2B%3D%20data%5Bi%5D%3B%0A” message=”java code” highlight=”” provider=”manual”/]The diagram shows why the branch predictor gets confused.
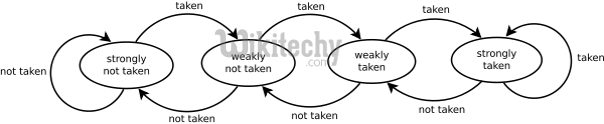
- Each element in the original code is a random value
- so the predictor will change sides as the std::rand() blow.
- Once it’s sorted, the predictor will first move into a state of strongly not taken and when the values change to the high value the predictor will in three runs through change all the way from strongly not taken to strongly taken.
nice try
nice