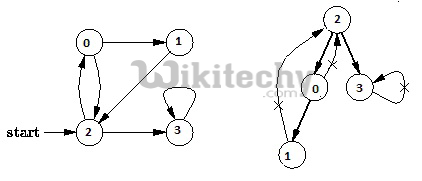
Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false. For example, the following graph contains three cycles 0->2->0, 0->1->2->0 and 3->3, so your function must return true.

Solution
Depth First Traversal can be used to detect cycle in a Graph. DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a back edge present in the graph. A back edge is an edge that is from a node to itself (selfloop) or one of its ancestor in the tree produced by DFS. In the following graph, there are 3 back edges, marked with cross sign. We can observe that these 3 back edges indicate 3 cycles present in the graph.

Detect Cycle in a directed graph using colors

In the previous post, we have discussed a solution that stores visited vertices in a separate array which stores vertices of current recursion call stack.

In this post a different solution is discussed. The solution is from CLRS book. The idea is to do DFS of given graph and while doing traversal, assign one of the below three colors to every vertex.

WHITE : Vertex is not processed yet.  Initially
        all vertices are WHITE.

GRAY : Vertex is being processed (DFS for this 
       vertex has started, but not finished which means
       that all descendants (ind DFS tree) of this vertex
       are not processed yet (or this vertex is in function
       call stack)

BLACK : Vertex and all its descendants are 
        processed.

While doing DFS, if we encounter an edge from current 
vertex to a GRAY vertex, then this edge is back edge 
and hence there is a cycle.

Below is C++ implementation based on above idea.

// A DFS based approach to find if there is a cycle
// in a directed graph.  This approach strictly follows
// the algorithm given in CLRS book.
#include <bits/stdc++.h>
using namespace std;
 
enum Color {WHITE, GRAY, BLACK};
 
// Graph class represents a directed graph using
// adjacency list representation
class Graph
{
    int V; // No. of vertices
    list<int>* adj; // adjacency lists
 
    // DFS traversal of the vertices reachable from v
    bool DFSUtil(int v, int color[]);
public:
    Graph(int V);  // Constructor
 
    // function to add an edge to graph
    void addEdge(int v, int w);
 
    bool isCyclic();
};
 
// Constructor
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}
 
// Utility function to add an edge
void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v's list.
}
 
// Recursive function to find if there is back edge
// in DFS subtree tree rooted with 'u'
bool Graph::DFSUtil(int u, int color[])
{
    // GRAY :  This vertex is being processed (DFS
    //         for this vertex has started, but not
    //         ended (or this vertex is in function
    //         call stack)
    color[u] = GRAY;
 
    // Iterate through all adjacent vertices
    list<int>::iterator i;
    for (i = adj[u].begin(); i != adj[u].end(); ++i)
    {
        int v = *i;  // An adjacent of u
 
        // If there is
        if (color[v] == GRAY)
          return true;
 
        // If v is not processed and there is a back
        // edge in subtree rooted with v
        if (color[v] == WHITE && DFSUtil(v, color))
          return true;
    }
 
    // Mark this vertex as processed
    color[u] = BLACK;
 
    return false;
}
 
// Returns true if there is a cycle in graph
bool Graph::isCyclic()
{
    // Initialize color of all vertices as WHITE
    int *color = new int[V];
    for (int i = 0; i < V; i++)
        color[i] = WHITE;
 
    // Do a DFS traversal beginning with all
    // vertices
    for (int i = 0; i < V; i++)
        if (color[i] == WHITE)
           if (DFSUtil(i, color) == true)
              return true;
 
    return false;
}
 
// Driver code to test above
int main()
{
    // Create a graph given in the above diagram
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);
 
    if (g.isCyclic())
        cout << "Graph contains cycle";
    else
        cout << "Graph doesn't contain cycle";
 
    return 0;
}

Output :

Graph contains cycle

Time complexity of above solution is O(V + E) where V is number of vertices and E is number of edges in the graph.

Categorized in:

Graph Cycle

Tagged in:

, , , , , , ,