Given a binary tree, print it vertically. The following example illustrates vertical order traversal.

           1
        /    \
       2      3
      / \    / \
     4   5  6   7
             \   \
              8   9 
               
			  
The output of print this tree vertically will be:
4
2
1 5 6
3 8
7
9

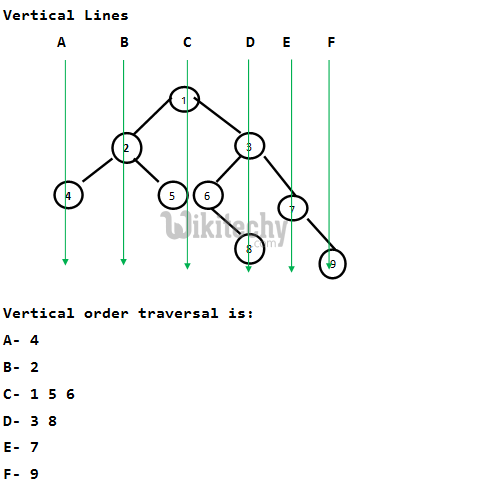
We have discussed a O(n²) solution in the previous post. In this post, an efficient solution based on hash map is discussed. We need to check the Horizontal Distances from root for all nodes. If two nodes have the same Horizontal Distance (HD), then they are on same vertical line. The idea of HD is simple. HD for root is 0, a right edge (edge connecting to right subtree) is considered as +1 horizontal distance and a left edge is considered as -1 horizontal distance. For example, in the above tree, HD for Node 4 is at -2, HD for Node 2 is -1, HD for 5 and 6 is 0 and HD for node 7 is +2.
We can do preorder traversal of the given Binary Tree. While traversing the tree, we can recursively calculate HDs. We initially pass the horizontal distance as 0 for root. For left subtree, we pass the Horizontal Distance as Horizontal distance of root minus 1. For right subtree, we pass the Horizontal Distance as Horizontal Distance of root plus 1. For every HD value, we maintain a list of nodes in a hasp map. Whenever we see a node in traversal, we go to the hash map entry and add the node to the hash map using HD as a key in map.

Following is C++ implementation of the above method. Thanks to Chirag for providing the below C++ implementation.

// C++ program for printing vertical order of a given binary tree
#include <iostream>
#include <vector>
#include <map>
using namespace std;
 
// Structure for a binary tree node
struct Node
{
    int key;
    Node *left, *right;
};
 
// A utility function to create a new node
struct Node* newNode(int key)
{
    struct Node* node = new Node;
    node->key = key;
    node->left = node->right = NULL;
    return node;
}
 
// Utility function to store vertical order in map 'm'
// 'hd' is horigontal distance of current node from root.
// 'hd' is initally passed as 0
void getVerticalOrder(Node* root, int hd, map<int, vector<int>> &m)
{
    // Base case
    if (root == NULL)
        return;
 
    // Store current node in map 'm'
    m[hd].push_back(root->key);
 
    // Store nodes in left subtree
    getVerticalOrder(root->left, hd-1, m);
 
    // Store nodes in right subtree
    getVerticalOrder(root->right, hd+1, m);
}
 
// The main function to print vertical oder of a binary tree
// with given root
void printVerticalOrder(Node* root)
{
    // Create a map and store vertical oder in map using
    // function getVerticalOrder()
    map < int,vector<int> > m;
    int hd = 0;
    getVerticalOrder(root, hd,m);
 
    // Traverse the map and print nodes at every horigontal
    // distance (hd)
    map< int,vector<int> > :: iterator it;
    for (it=m.begin(); it!=m.end(); it++)
    {
        for (int i=0; i<it->second.size(); ++i)
            cout << it->second[i] << " ";
        cout << endl;
    }
}
 
// Driver program to test above functions
int main()
{
    Node *root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->right->left = newNode(6);
    root->right->right = newNode(7);
    root->right->left->right = newNode(8);
    root->right->right->right = newNode(9);
    cout << "Vertical order traversal is \n";
    printVerticalOrder(root);
    return 0;
}

Output:

Vertical order traversal is
4
2
1 5 6
3 8
7
9

Time Complexity of hashing based solution can be considered as O(n) under the assumption that we have good hashing function that allows insertion and retrieval operations in O(1) time. In the above C++ implementation, map of STL is used. map in STL is typically implemented using a Self-Balancing Binary Search Tree where all operations take O(Logn) time. Therefore time complexity of above implementation is O(nLogn).

Note that the above solution may print nodes in same vertical order as they appear in tree. For example, the above program prints 12 before 9. See this for a sample run.

             1
          /     \
         2       3
        /  \    /  \
       4    5  6    7
                \  /  \
                 8 10  9 
                     \
                     11
                       \
                        12