Given a graph and a source vertex src in graph, find shortest paths from src to all vertices in the given graph. The graph may contain negative weight edges.
We have discussed Dijkstra’s algorithm for this problem. Dijksra’s algorithm is a Greedy algorithm and time complexity is O(VLogV) (with the use of Fibonacci heap). Dijkstra doesn’t work for Graphs with negative weight edges, Bellman-Ford works for such graphs. Bellman-Ford is also simpler than Dijkstra and suites well for distributed systems. But time complexity of Bellman-Ford is O(VE), which is more than Dijkstra.

Algorithm
Following are the detailed steps.

Input: Graph and a source vertex src
Output: Shortest distance to all vertices from src. If there is a negative weight cycle, then shortest distances are not calculated, negative weight cycle is reported.

• This step initializes distances from source to all vertices as infinite and distance to source itself as 0. Create an array dist[] of size |V| with all values as infinite except dist[src] where src is source vertex.
• This step calculates shortest distances. Do following |V|-1 times where |V| is the number of vertices in given graph.
  • …..Do following for each edge u-v
    ………………If dist[v] > dist[u] + weight of edge uv, then update dist[v] ………………….dist[v] = dist[u] + weight of edge uv
• This step reports if there is a negative weight cycle in graph. Do following for each edge u-v
  ……If dist[v] > dist[u] + weight of edge uv, then “Graph contains negative weight cycle”
  The idea of step 3 is, step 2 guarantees shortest distances if graph doesn’t contain negative weight cycle. If we iterate through all edges one more time and get a shorter path for any vertex, then there is a negative weight cycle

How does this work? Like other Dynamic Programming Problems, the algorithm calculate shortest paths in bottom-up manner. It first calculates the shortest distances for the shortest paths which have at-most one edge in the path. Then, it calculates shortest paths with at-nost 2 edges, and so on. After the ith iteration of outer loop, the shortest paths with at most i edges are calculated. There can be maximum |V| – 1 edges in any simple path, that is why the outer loop runs |v| – 1 times. The idea is, assuming that there is no negative weight cycle, if we have calculated shortest paths with at most i edges, then an iteration over all edges guarantees to give shortest path with at-most (i+1) edges.

Example
Let us understand the algorithm with following example graph. The images are taken from this source.

Let the given source vertex be 0. Initialize all distances as infinite, except the distance to source itself. Total number of vertices in the graph is 5, so all edges must be processed 4 times.

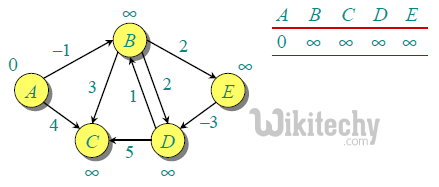
Let all edges are processed in following order: (B,E), (D,B), (B,D), (A,B), (A,C), (D,C), (B,C), (E,D). We get following distances when all edges are processed first time. The first row in shows initial distances. The second row shows distances when edges (B,E), (D,B), (B,D) and (A,B) are processed. The third row shows distances when (A,C) is processed. The fourth row shows when (D,C), (B,C) and (E,D) are processed.

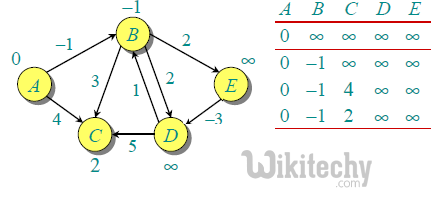
The first iteration guarantees to give all shortest paths which are at most 1 edge long. We get following distances when all edges are processed second time (The last row shows final values).

The second iteration guarantees to give all shortest paths which are at most 2 edges long. The algorithm processes all edges 2 more times. The distances are minimized after the second iteration, so third and fourth iterations don’t update the distances.

// A C / C++ program for Bellman-Ford's single source 
// shortest path algorithm.
 
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
 
// a structure to represent a weighted edge in graph
struct Edge
{
    int src, dest, weight;
};
 
// a structure to represent a connected, directed and 
// weighted graph
struct Graph
{
    // V-> Number of vertices, E-> Number of edges
    int V, E;
 
    // graph is represented as an array of edges.
    struct Edge* edge;
};
 
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
    struct Graph* graph = 
         (struct Graph*) malloc( sizeof(struct Graph) );
    graph->V = V;
    graph->E = E;
 
    graph->edge = 
       (struct Edge*) malloc( graph->E * sizeof( struct Edge ) );
 
    return graph;
}
 
// A utility function used to print the solution
void printArr(int dist[], int n)
{
    printf("Vertex   Distance from Source\n");
    for (int i = 0; i < n; ++i)
        printf("%d \t\t %d\n", i, dist[i]);
}
 
// The main function that finds shortest distances from src to
// all other vertices using Bellman-Ford algorithm.  The function
// also detects negative weight cycle
void BellmanFord(struct Graph* graph, int src)
{
    int V = graph->V;
    int E = graph->E;
    int dist[V];
 
    // Step 1: Initialize distances from src to all other vertices
    // as INFINITE
    for (int i = 0; i < V; i++)
        dist[i]   = INT_MAX;
    dist[src] = 0;
 
    // Step 2: Relax all edges |V| - 1 times. A simple shortest 
    // path from src to any other vertex can have at-most |V| - 1 
    // edges
    for (int i = 1; i <= V-1; i++)
    {
        for (int j = 0; j < E; j++)
        {
            int u = graph->edge[j].src;
            int v = graph->edge[j].dest;
            int weight = graph->edge[j].weight;
            if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
                dist[v] = dist[u] + weight;
        }
    }
 
    // Step 3: check for negative-weight cycles.  The above step 
    // guarantees shortest distances if graph doesn't contain 
    // negative weight cycle.  If we get a shorter path, then there
    // is a cycle.
    for (int i = 0; i < E; i++)
    {
        int u = graph->edge[i].src;
        int v = graph->edge[i].dest;
        int weight = graph->edge[i].weight;
        if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
            printf("Graph contains negative weight cycle");
    }
 
    printArr(dist, V);
 
    return;
}
 
// Driver program to test above functions
int main()
{
    /* Let us create the graph given in above example */
    int V = 5;  // Number of vertices in graph
    int E = 8;  // Number of edges in graph
    struct Graph* graph = createGraph(V, E);
 
    // add edge 0-1 (or A-B in above figure)
    graph->edge[0].src = 0;
    graph->edge[0].dest = 1;
    graph->edge[0].weight = -1;
 
    // add edge 0-2 (or A-C in above figure)
    graph->edge[1].src = 0;
    graph->edge[1].dest = 2;
    graph->edge[1].weight = 4;
 
    // add edge 1-2 (or B-C in above figure)
    graph->edge[2].src = 1;
    graph->edge[2].dest = 2;
    graph->edge[2].weight = 3;
 
    // add edge 1-3 (or B-D in above figure)
    graph->edge[3].src = 1;
    graph->edge[3].dest = 3;
    graph->edge[3].weight = 2;
 
    // add edge 1-4 (or A-E in above figure)
    graph->edge[4].src = 1;
    graph->edge[4].dest = 4;
    graph->edge[4].weight = 2;
 
    // add edge 3-2 (or D-C in above figure)
    graph->edge[5].src = 3;
    graph->edge[5].dest = 2;
    graph->edge[5].weight = 5;
 
    // add edge 3-1 (or D-B in above figure)
    graph->edge[6].src = 3;
    graph->edge[6].dest = 1;
    graph->edge[6].weight = 1;
 
    // add edge 4-3 (or E-D in above figure)
    graph->edge[7].src = 4;
    graph->edge[7].dest = 3;
    graph->edge[7].weight = -3;
 
    BellmanFord(graph, 0);
 
    return 0;
}

Output :

Vertex   Distance from Source
0                0
1                -1
2                2
3                -2
4                1

Notes

• Negative weights are found in various applications of graphs. For example, instead of paying cost for a path, we may get some advantage if we follow the path.
• Bellman-Ford works better (better than Dijksra’s) for distributed systems. Unlike Dijksra’s where we need to find minimum value of all vertices, in Bellman-Ford, edges are considered one by one.