Binary Search
We can use binary search to reduce the number of comparisons in normal insertion sort. Binary Insertion Sort find use binary search to find the proper location to insert the selected item at each iteration.
In normal insertion, sort it takes O(i) (at ith iteration) in worst case. we can reduce it to O(logi) by using binary search.
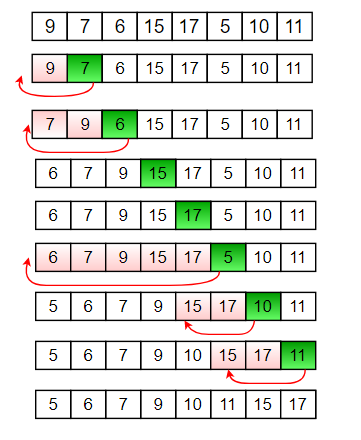
diagram for binary insertion sort
Implementation of Binary Insertion Sort in C
C
// C program for implementation of binary insertion sort
#include <stdio.h>
// A binary search based function to find the position
// where item should be inserted in a[low..high]
int binarySearch(int a[], int item, int low, int high)
{
if (high <= low)
return (item > a[low])? (low + 1): low;
int mid = (low + high)/2;
if(item == a[mid])
return mid+1;
if(item > a[mid])
return binarySearch(a, item, mid+1, high);
return binarySearch(a, item, low, mid-1);
}
// Function to sort an array a[] of size 'n'
void insertionSort(int a[], int n)
{
int i, loc, j, k, selected;
for (i = 1; i < n; ++i)
{
j = i - 1;
selected = a[i];
// find location where selected sould be inseretd
loc = binarySearch(a, selected, 0, j);
// Move all elements after location to create space
while (j >= loc)
{
a[j+1] = a[j];
j--;
}
a[j+1] = selected;
}
}
// Driver program to test above function
int main()
{
int a[] = {37, 23, 0, 17, 12, 72, 31,
46, 100, 88, 54};
int n = sizeof(a)/sizeof(a[0]), i;
insertionSort(a, n);
printf("Sorted array: \n");
for (i = 0; i < n; i++)
printf("%d ",a[i]);
return 0;
}
Output:
Sorted array:
0 12 17 23 31 37 46 54 72 88 100
Time Complexity: The algorithm as a whole still has a running worst case running time of O(n2) because of the series of swaps required for each insertion.
[ad type=”banner”]
Implementation of Binary Insertion Sort in JAVA
In this implementation, I have used library functions for binary search and shifting array to one location right
package com.codingeek.algorithms.sorting;
import java.util.Arrays;
class BinaryInsertionSort{
public static void main(String[] args) {
final int[] input = { 4, 10, 3, 1, 9, 15 };
System.out.println("Before Sorting - " + Arrays.toString(input));
new BinaryInsertionSort().sort(input);
System.out.println("After Sorting - " + Arrays.toString(input));
}
public void sort(int array[]) {
for (int i = 1; i < array.length; i++) {
int x = array[i];
// Find location to insert using binary search
int j = Math.abs(Arrays.binarySearch(array, 0, i, x) + 1);
//Shifting array to one location right
System.arraycopy(array, j, array, j+1, i-j);
//Placing element at its correct location
array[j] = x;
}
}
Output:-
Before Sorting - [4, 10, 3, 1, 9, 15]
After Sorting - [1, 3, 4, 9, 10, 15]
