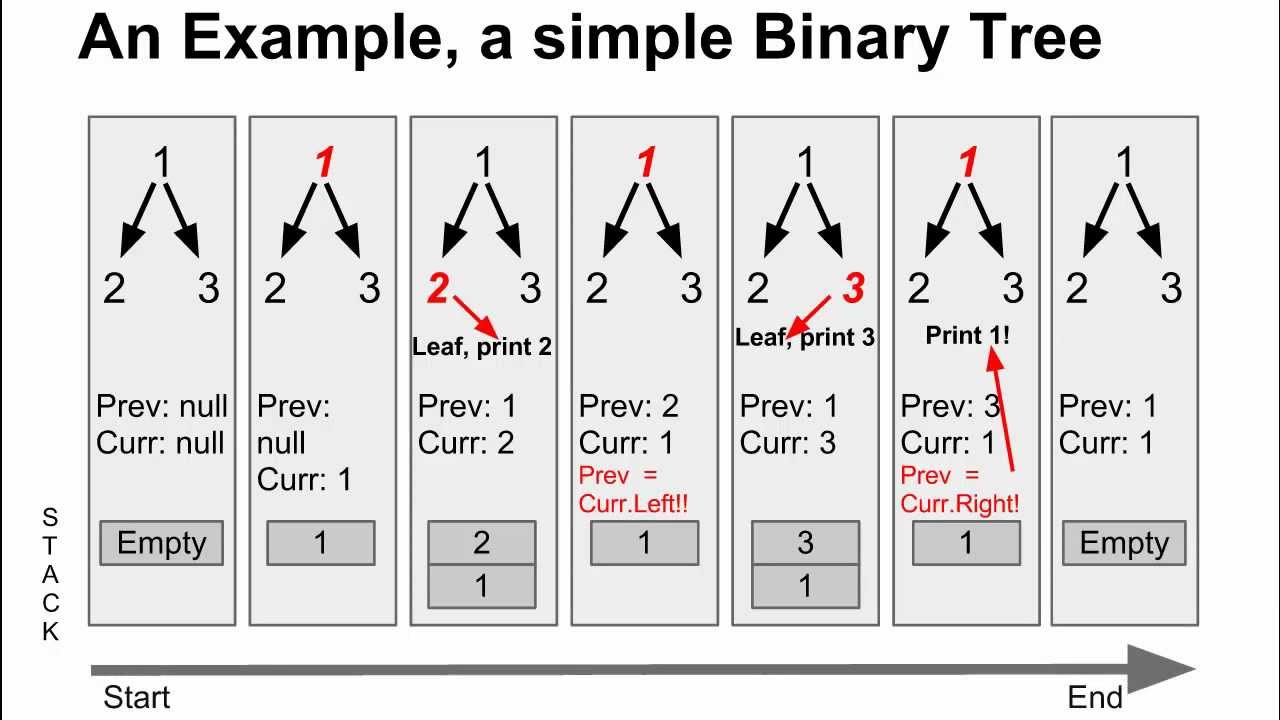
Using Morris Traversal, we can traverse the tree without using stack and recursion. The idea of Morris Traversal is based on Threaded Binary Tree. In this traversal, we first create links to Inorder successor and print the data using these links, and finally revert the changes to restore original tree.
1. Initialize current as root
2. While current is not NULL
If current does not have left child
a) Print current’s data
b) Go to the right, i.e., current = current->right
Else
a) Make current as right child of the rightmost
node in current's left subtree
b) Go to this left child, i.e., current = current->left
Although the tree is modified through the traversal, it is reverted back to its original shape after the completion. Unlike Stack based traversal, no extra space is required for this traversal.
# Python program to do inorder traversal without recursion and
# without stack Morris inOrder Traversal
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Iterative function for inorder tree traversal
def MorrisTraversal(root):
# Set current to root of binary tree
current = root
while(current is not None):
if current.left is None:
print current.data ,
current = current.right
else:
#Find the inorder predecessor of current
pre = current.left
while(pre.right is not None and pre.right != current):
pre = pre.right
# Make current as right child of its inorder predecessor
if(pre.right is None):
pre.right = current
current = current.left
# Revert the changes made in if part to restore the
# original tree i.e., fix the right child of predecssor
else:
pre.right = None
print current.data ,
current = current.right
# Driver program to test above function
"""
Constructed binary tree is
1
/ \
2 3
/ \
4 5
"""
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
MorrisTraversal(root)
# This code is contributed by Naveen Aili
Output:
4 2 5 1 3
