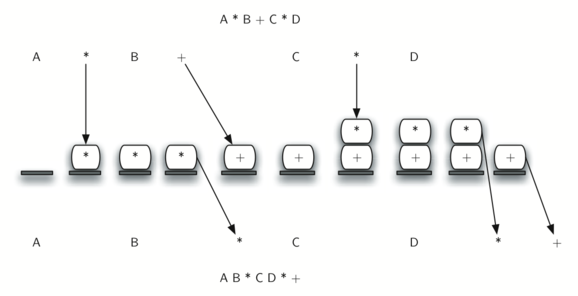
Infix expression:
- The expression of the form a op b. When an operator is in-between every pair of operands.
Postfix expression:
- The expression of the form a b op. When an operator is followed for every pair of operands.
Why postfix representation of the expression?
- The compiler scans the expression either from left to right or from right to left.
Consider the below expression:
a op1 b op2 c op3 d
If op1 = +, op2 = *, op3 = +
The compiler first scans the expression to evaluate the expression b * c, then again scan the expression to add a to it. The result is then added to d after another scan.
The repeated scanning makes it very in-efficient. It is better to convert the expression to postfix(or prefix) form before evaluation.
The corresponding expression in postfix form is: abc*+d+. The postfix expressions can be evaluated easily using a stack. We will cover postfix expression evaluation in a separate post.
[ad type=”banner”]
Algorithm
1. Scan the infix expression from left to right.
2. If the scanned character is an operand, output it.
3. Else,
—->3.1 If the precedence of the scanned operator is greater than the precedence of the operator in the stack(or the stack is empty), push it.
—–>3.2 Else, Pop the operator from the stack until the precedence of the scanned operator is less-equal to the precedence of the operator residing on the top of the stack. Push the scanned operator to the stack.
4. If the scanned character is an ‘(‘, push it to the stack.
5. If the scanned character is an ‘)’, pop and output from the stack until an ‘(‘ is encountered.
6. Repeat steps 2-6 until infix expression is scanned.
7. Pop and output from the stack until it is not empty.
Following is C implementation of the above algorithm
Python Programming:
# Python program to convert infix expression to postfix
# Class to convert the expression
class Conversion:
# Constructor to initialize the class variables
def __init__(self, capacity):
self.top = -1
self.capacity = capacity
# This array is used a stack
self.array = []
# Precedence setting
self.output = []
self.precedence = {'+':1, '-':1, '*':2, '/':2, '^':3}
# check if the stack is empty
def isEmpty(self):
return True if self.top == -1 else False
# Return the value of the top of the stack
def peek(self):
return self.array[-1]
# Pop the element from the stack
def pop(self):
if not self.isEmpty():
self.top -= 1
return self.array.pop()
else:
return "$"
# Push the element to the stack
def push(self, op):
self.top += 1
self.array.append(op)
# A utility function to check is the given character
# is operand
def isOperand(self, ch):
return ch.isalpha()
# Check if the precedence of operator is strictly
# less than top of stack or not
def notGreater(self, i):
try:
a = self.precedence[i]
b = self.precedence[self.peek()]
return True if a <= b else False
except KeyError:
return False
# The main function that converts given infix expression
# to postfix expression
def infixToPostfix(self, exp):
# Iterate over the expression for conversion
for i in exp:
# If the character is an operand,
# add it to output
if self.isOperand(i):
self.output.append(i)
# If the character is an '(', push it to stack
elif i == '(':
self.push(i)
# If the scanned character is an ')', pop and
# output from the stack until and '(' is found
elif i == ')':
while( (not self.isEmpty()) and self.peek() != '('):
a = self.pop()
self.output.append(a)
if (not self.isEmpty() and self.peek() != '('):
return -1
else:
self.pop()
# An operator is encountered
else:
while(not self.isEmpty() and self.notGreater(i)):
self.output.append(self.pop())
self.push(i)
# pop all the operator from the stack
while not self.isEmpty():
self.output.append(self.pop())
print "".join(self.output)
# Driver program to test above function
exp = "a+b*(c^d-e)^(f+g*h)-i"
obj = Conversion(len(exp))
obj.infixToPostfix(exp)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
[ad type=”banner”]
Output:
abcd^e-fgh*+^*+i-
